Доказать что треугольник равнобедренный

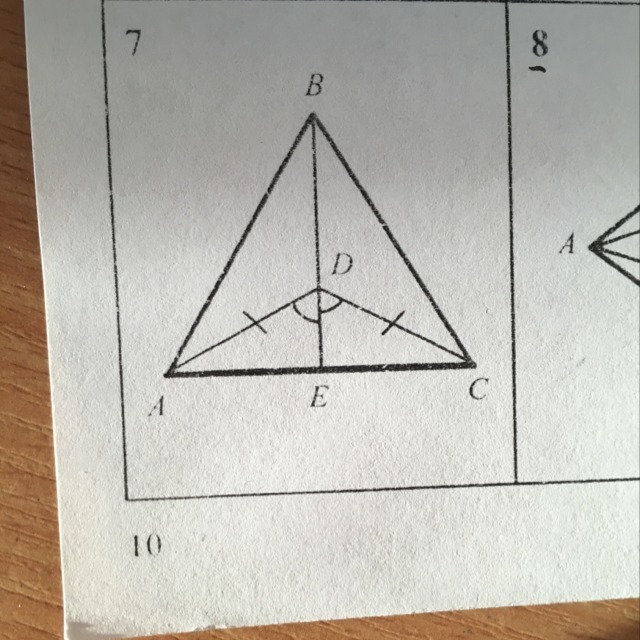
/_ ADE=/_EDC
DE=Общий
AD=DC
ПО ПЕРВОМУ ПРИЗНАКУ РАВЕНСТВА ТР.
Из этого следует что треугольник ADE=треугольнику EDC
ИЗ этого следует, что AE=EC
Значит BE= МЕДИАНА
AE=EC
BE=Общий
/_AED=/_CED
ПО ПЕРВОМУ ПРИЗНАКУ РАВЕНСТВА ТР.
Из этого следует, что треуг. ABE=треуг. EBC
ИЗ ЭТОГО СЛЕДУЕТ, ЧТО AB=BC #
МЫ ДОКАЗАЛИ
ПЛИЗЗ, ОТМЕТЬ КАК ЛУЧШИЙ ОТВЕТ

ΔADC равнобедренный (по условию), DE биссектриса ∠D;

В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой. Следовательно ED - серединный перпендикуляр к АС.

Все точки принадлежащие серединному перпендикуляру равноудалены от концов отрезка к которому он проведен.

В принадлежит серединному перпендикуляру проведенному к АС, следовательно АВ=ВС, ⇒ АВС - равнобедренный.

Если Вам не сложно....Помогите мне тоже пожалуйста....Я Вас оочень прошу....https://znanija.com/task/30763532