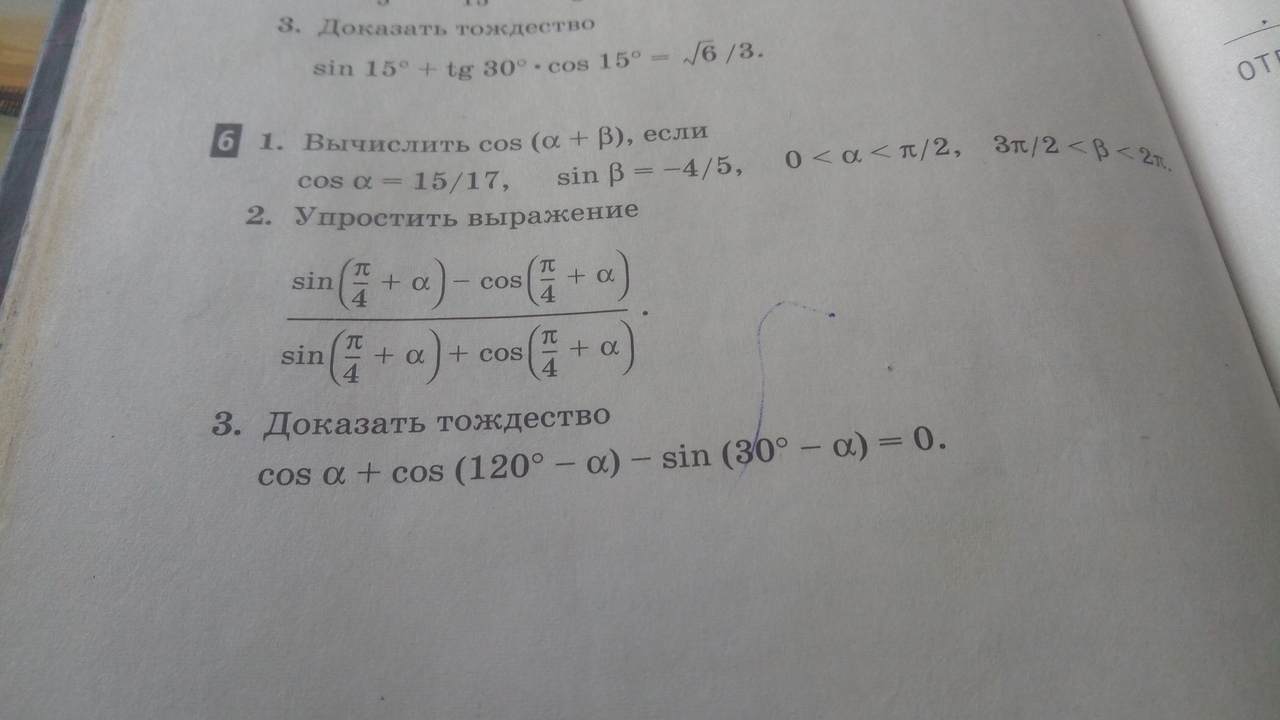тригонометрия, мне нужно до завтра пожалуйста.

Ответ:

Пошаговое объяснение:

1) Из основного тригонометрического тождества sin^2 + cos^2 = 1, найдем, что sinα=±8/17. Т.к. угол α расположен в первом квадранте, где синус положителен, то sinα=8/17

Аналогично найдем, что cosβ=±3/5. Угол β по условию расположен в четвертом квадранте и следовательно cosβ=3/5

По формуле косинуса суммы:

cos(α+β) = cosαcosβ - sinαsinβ = 15/17 * 3/5 - 8/17 * (-4/5) = 45/85 + 32/85 = 77/85

2) Применим формулы синуса и косинуса суммы:

Т.к. , то можем сократить на него получим:

3) Применим формулы косинуса и синуса разности: