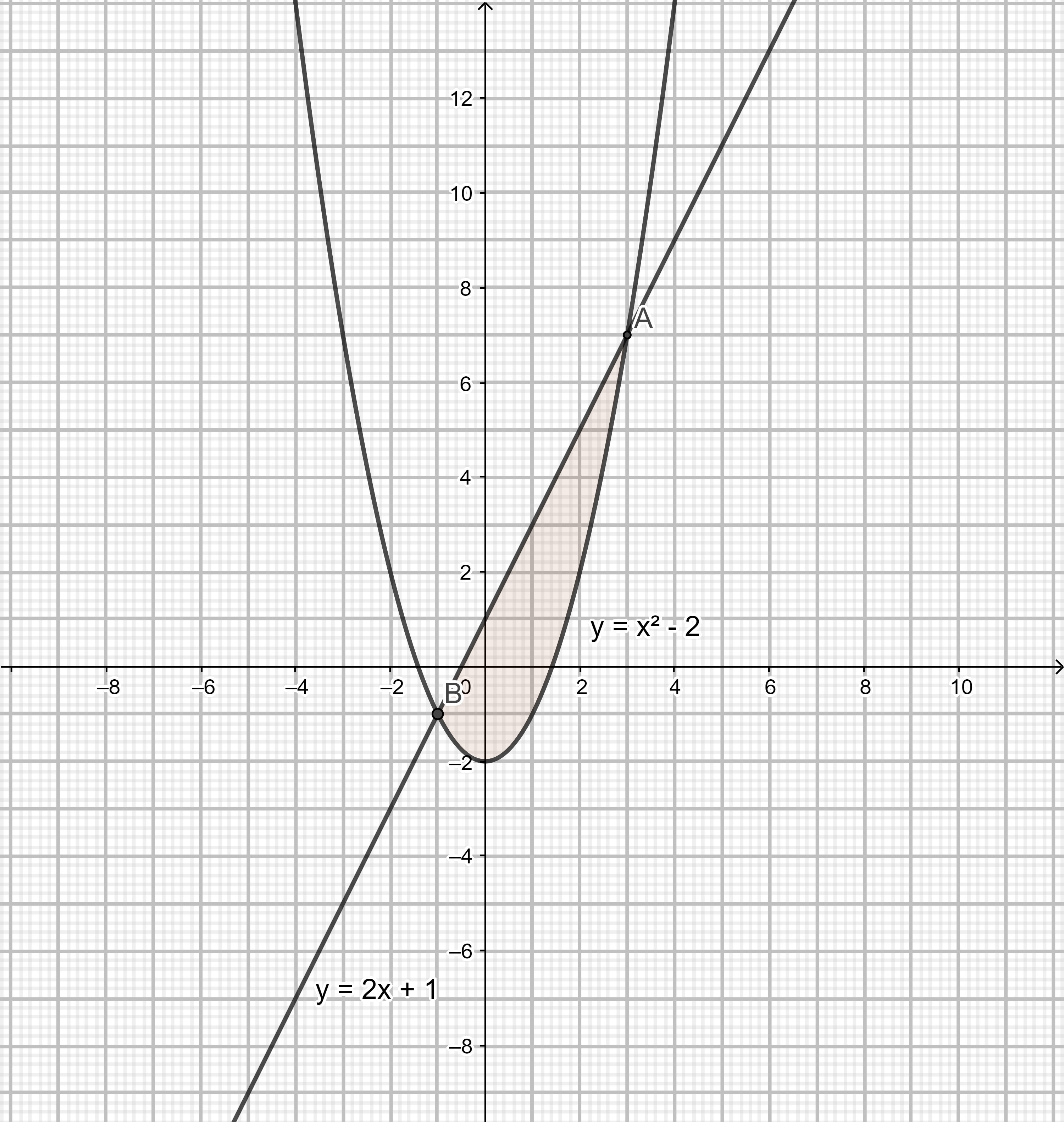
Вычислить площадь фигуры, ограниченной линиями y=x^2-2, y=2x+1. Нарисуйте графики и заштрихуйте фигуру.

Ответы

Ответ дал: kiramaxx

Ответ:

10,7

Пошаговое объяснение:

Требуется вычислить площадь, заключенную между параболой y=x^2-2 и прямой y=2x+1.

Найдем точки пересечения параболы и прямой:

$[left{ begin{array}{l}y = {x^2} - 2\y = 2x + 1end{array} right. Leftrightarrow left{ begin{array}{l}2x + 1 = {x^2} - 2\y = 2x + 1end{array} right. Leftrightarrow left{ begin{array}{l}2x + 1 - {x^2} + 2 = 0\y = 2x + 1end{array} right. Leftrightarrow left{ begin{array}{l} - {x^2} + 2x + 3 = 0\y = 2x + 1end{array} right.]% MathType!End!2!1!$

$- {x^2} + 2x + 3=0$

Найдем дискриминант квадратного уравнения:

$D = {b^2} - 4a = {2^2} - 4( - 1)*3 = 4 + 12 = 16$

${x_{1,2}} = frac{{ - b pm sqrt {{b^2} - 4ac} }}{{2a}}$

${x_1} = frac{{ - 2 - sqrt {16} }}{{2*( - 1)}} = frac{{ - 2 - 4}}{{ - 2}} = frac{{ - 6}}{{ - 2}} = 3$

${x_2} = frac{{ - 2 + sqrt {16} }}{{2*( -1)}} = frac{{-2+ 4}}{{- 2}} = frac{2}{{-2}} =-1$

Подставим x в уравнение:

y₁=7; y₂=-1

Получаем две точки пересечения : (3;7) и (-1;-1)

Пределы интегрирования a=-1, b=3. Площадь фигуры равняется:

$S = intlimits_{- 1}^3 {(2x + 1) - ({x^2} - 2)dx =} intlimits_{-1}^3 (-{x^2} + 2x + 3)dx =$

$= - intlimits_{- 1}^3 {{x^2}dx + } 2intlimits_{- 1}^3 {x *dx}+3intlimits_{- 1}^3 {1 *dx}=- left. {frac{{{x^3}}}{3}} right|_{- 1}^3 + 2left. {frac{{{x^2}}}{2}} right|_{- 1}^3+3left. {frac{x}{1}} right|_{ - 1}^3$