Ответы
Ответ дал:
0
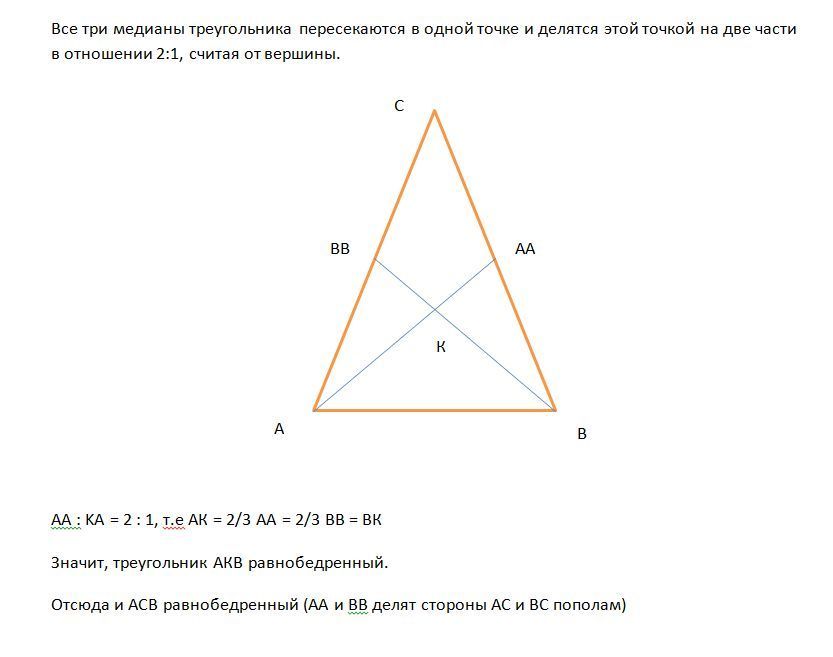
Доказательсьво опирается на то, что три медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Приложения:
Ответ дал:
0
"отсюда и АСВ равнобедренный" - сразу не следует из равнобедренности АКВ. Пропущено одно звено доказательства..
Ответ дал:
0
да, Вы правы. надо опустить медиану из угла С на АВ в точку СС. В треуг АКВ она же будет и высота, т.к он равнобедренный. но тогда и медиана С СС будет высотой в треуг АВС. т.е. АВС - равнобедренный.
Ответ дал:
0
не, там ничего опускать не надо. Пропущенное звено такое - АКВ- равнобедренный - углы у него при основании равны - рассмотрим А.В.ВВ и А.В.АА у них стороны равны как общие (АВ) и по условию (медианы исходного треугольника) и углы между ними равны, значит и треуг. равны. - ну и тогда А.ВВ=В.АА , а это половины сторон АС и ВС, значит и АС=ВС
Ответ дал:
0
либо так как у вас - опустить высоту....
Ответ дал:
0
да, путей доказательства несколько. надеюсь, хоть одно из наших с Вами доказательств подойдет -))))
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад