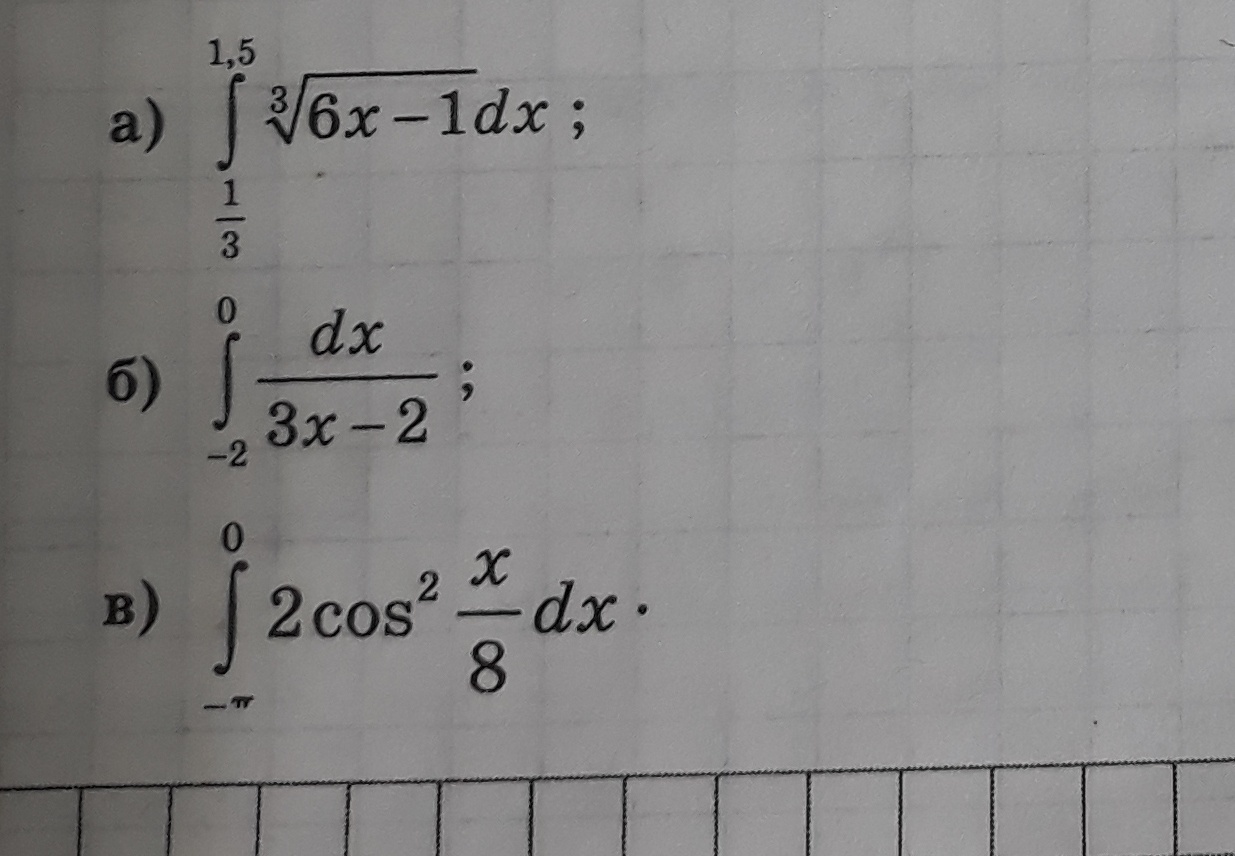Предмет: Математика
Автор: Kkkkkkoo
Вопрос задан 7 лет назад

< >

Помогите, пожалуйста)

Приложения:

Ответы

Ответ дал: mionkaf1

0

Ответ:

test

Пошаговое объяснение:

Определенные интегралы будем решать за формулой Ньютона — Лейбница

Не буду писать определенные интегралы, сразу нахожу неопределенные:

P.S будет проще сделать подстановкой

a)

$int sqrt[3]{6x-1}*dx\ \t=6x-1\ \ \int frac{1}{6} sqrt[3]{t}*dt =frac{1}{6} intsqrt[3]{t}*dt=frac{1}{6} int t^{frac{1}{3} }*dt=frac{1}{6}*frac{3tsqrt[3]{t} }{4}\ \Obr.zamena:\ \ \frac{1}{6}*frac{3(6x-1)sqrt[3]{6x-1} }{4} =frac{(6x-1)sqrt[3]{6x-1} }{8} ^{1.5}_{1/3}=frac{(6*1,5-1)sqrt[3]{6*1.5-1} }{8}-frac{(6*frac{1}{3}-1)sqrt[3]{6*frac{1}{3}-1 }}{8}\ \ \=frac{15}{8}$

б)

$int frac{1}{3x-2}*dx\ \ \t=3x-2\ \int frac{1}{3t}*dt=frac{1}{3} int frac{1}{t}*dt=frac{1}{3}*ln |t|=frac{1}{3}*ln|3x-2|^0_{-2}=\ \ =frac{1}{3}*ln|3*0-2|-frac{1}{3}*ln|3*(-2)-2|=-frac{2}{3}*ln2$

в)

$int 2cos^2(frac{x}{8})*dx\ \t=frac{x}{8} \ \2*int 8cos^2(t)*dt=16*intfrac{1+cos(2t)}{2}*dt=8(int1*dt+int cos(2t)*dt )=\ \=8(t+frac{sin(2t)}{2}=8(frac{x}{8}+frac{sin(2*frac{x}{8}) }{2})=x+4sin(frac{x}{4} )^0_{-pi}\ \0+4sin(frac{0}{4})-(-pi+sin(frac{-pi}{4}))=pi+2sqrt{2}$

Ответ дал: Kkkkkkoo

0

Спасибо большое)

Похожие вопросы

Окружающий мир

2 года назад

помогите пожалуйста срочно

Қазақ тiлi

2 года назад

саяхатшылар ози келген елдин салт дастурин сактауы миндеттиме

Русский язык

2 года назад

Образуй от глаголов действительные причастия прошедшего времени (м. р., ед. ч., И. п.). Пример: свистеть — свистевший; затихать — ; обнаружить — ; залезть — ; колоть — .

Математика

2 года назад

Найдите значение выражения: -3:5 целых 1/4 - 2 целых 1/2 : 7/8 даю 35 Баллов.

Математика

8 лет назад

82-15= надо решить разложив на десятки и единицы для 2-го класса

Математика

8 лет назад

помогитееее пожалуйста

Биология

9 лет назад

расположить этапы биосинтеза белка в правильном порядке 1 процессинг РНК 2 трансляция 3 транскрипция 4 фолдинг 5 дозревание белка в комплексе Гольджи

Математика

9 лет назад

Надо вставить числа в примеры в столбик. Впринципе легко,но попались такие примеры: #48 +1## #23 _____ 836. Как такие решать?