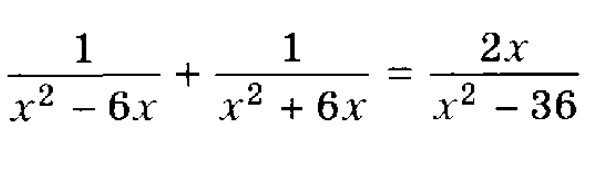Предмет: Алгебра
Автор: annadeevans
Вопрос задан 7 лет назад

Подскажите пожалуйста, как решать такие уравнения.. Что надо делать? 8 класс

Приложения:

Ответы

Ответ дал: Universalka

$frac{1}{x^{2}-6x }+frac{1}{x^{2}+6x } =frac{2x}{x^{2}-36 }\\frac{1}{x(x-6)}+frac{1}{x(x+6)}-frac{2x}{(x-6)(x+6)}=0\\frac{x+6+x-6-2x^{2} }{x(x-6)(x+6)}=0\\left { {{-2x^{2}+2x=0 }atop {x(x-6)(x+6)neq0 }} right.\\left { {{x^{2}-x=0 } atop {xneq 0;xneq-6;xneq6}} right.\\left { {{x(x-1)=0} atop {xneq0;xneq -6;xneq6}} right.\\x-1=0\\x=1$

Ответ дал: annadeevans

Блин, точно совсем забыла, спасибо!

Ответ дал: nadelyaev2002

Перво-наперво ищешь ОДЗ, то есть исключаешь те значения, при которым знаменатель обращается в ноль:

$x^2-36neq 0\xneq бsqrt{36} \xneq =-6;xneq 6;xneq0.$

Затем приводим левую и правую часть к общему знаменателю:

$frac{1}{x^2-6x} +frac{1}{x^2+6x} =frac{2x}{x^2-36} \frac{1}{x(x-6)} +frac{1}{x(x+6)} =frac{2x}{x^2-36}\frac{x+6+x-6}{x(x-6)(x+6)} =frac{2x^2}{x(x^2-36)}\frac{2x}{x(x^2-36)} =frac{2x^2}{x(x^2-36)}.$

Потом и левую и правую часть умножаем на этот знаменатель, чтобы избавиться от него, далее находим корни получившегося уравнения:

$2x=2x^2\2x^2-2x=0\2x(x-1)=0\x_1=0;x_2=1.$

Возвращаемся к ОДЗ и проверяем, не равняются ли корни уравнения его значениям. Если да, то исключаем их. В нашем случае - это ноль. Исключив его, мы получим 1. Это и есть ответ.

Ответ дал: annadeevans

Спасибо!)

Похожие вопросы

Русский язык

2 года назад

Составьте словосочетание, где первое слово на букву "с", а второе слово "заблуждение(я)"

Окружающий мир

2 года назад

какая вода в мировом океане более холодная:природная или поверхностная?

Химия

2 года назад

можно краткий но понятный ответ пожалуйста Что образуется когда горят вещества?