Докажите, что в равных треугольниках медианы,

проведенные к соответственным сторонам, равны

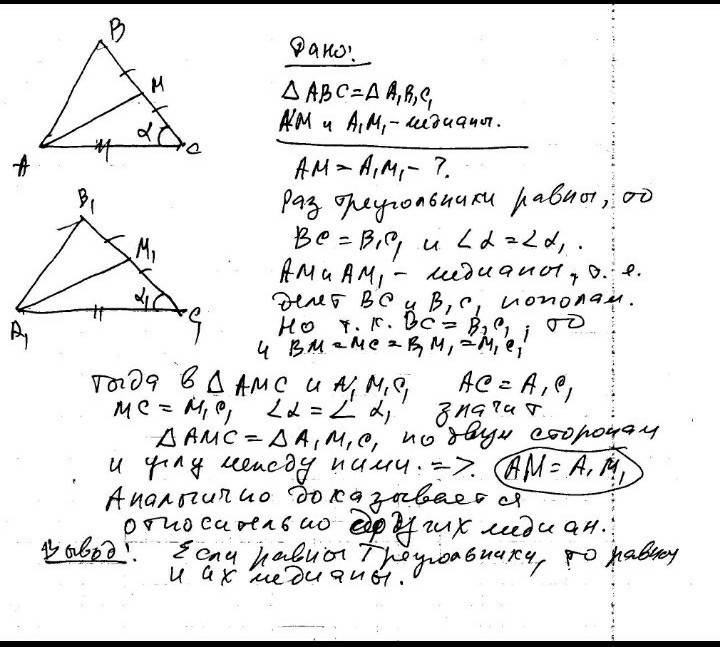
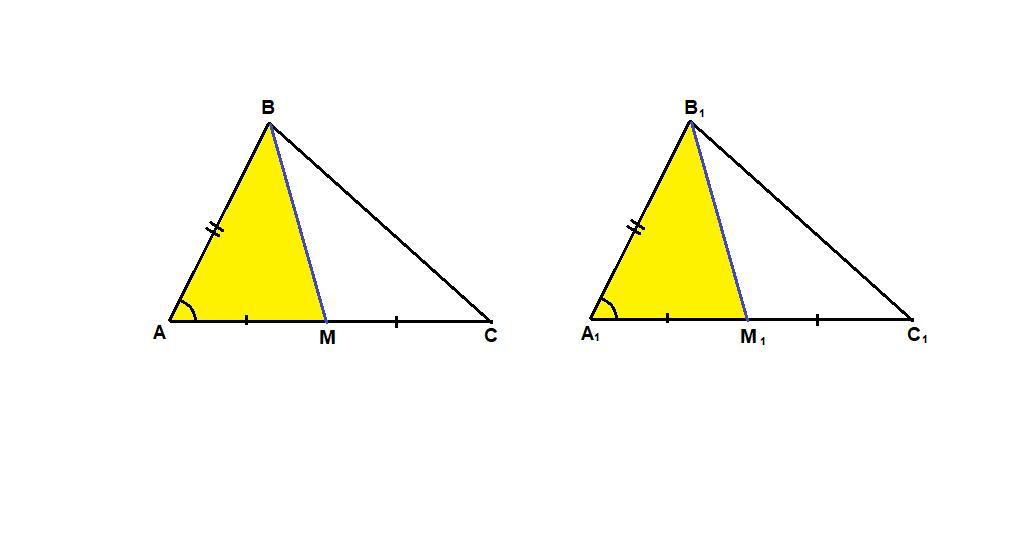
Ответ:

Дано: ΔАВС = ΔА₁В₁С₁, ВМ и В₁М₁ - медианы.

Доказать: ВМ = В₁М₁.

Доказательство:

АВ = А₁В₁ как соответствующие стороны равных треугольников,

∠А = ∠А₁ как соответствующие углы равных треугольников,

АМ = 1/2 АС        А₁М₁ = 1/2 А₁С₁,  а так как АС = А₁С₁, то и

АМ = А₁М₁, значит

ΔАВМ = ΔА₁В₁М₁ по двум сторонам и углу между ними.

В равных треугольниках напротив равных углов лежат равные стороны, значит ВМ = В₁М₁.