В равнобедренном треугольнике проведена к основанию биссектриса. Доказать равенство получившихся треугольников
Ответы
Ответ дал:
0
Дано:
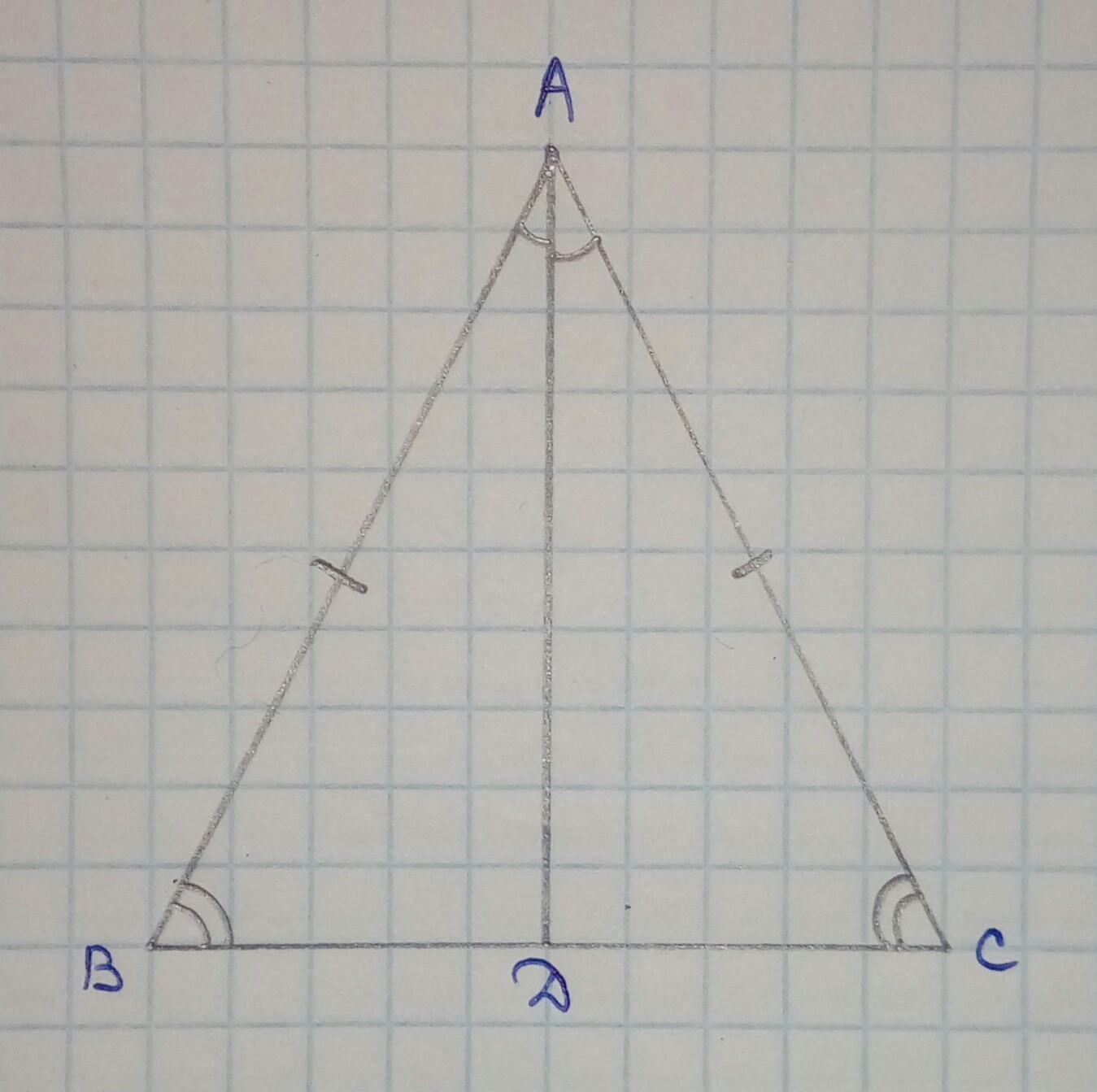
∆ ABC - равнобед.
AD - биссектриса
Доказать: ∆ ABD = ∆ ACD.
Док-во.
Рассмотрим ∆ ABC. Т.к. он равнобед. с осн. BC, то стороны AB=AC и ∠ABD =∠ACD ( как углы при основании )
Проведена биссектриса AD, которая делит угол пополам.
Значит, ∠DAB =∠DAC.
А т.к. AB=AC, ∠ABD =∠ACD, ∠DAB =∠DAC, то ∆ ABD = ∆ ACD ( по Ⅱ пр. р. тр. )
Доказано.
Приложения:
Ответ дал:
0
спасибо)
Ответ дал:
0
Пожалуйста) можешь назвать лучшим ответом?
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад