Предмет: Геометрия
Автор: Sekret666
Вопрос задан 7 лет назад

< >

радиусы оснований усечённого конуса равны 8 и 12 см а образующая составляет с плоскостью основания угол 25 градусов чему равна площадь боковой поверхности этого конуса

Ответы

Ответ дал: as11111

0

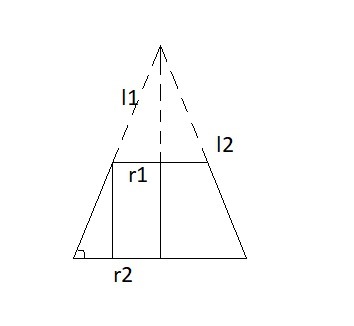
Если обозначим радиусы оснований через $r_1$ (меньшее) и $r_2$ (большее), а образующую усеченной части конуса через $l_1$ и образующую большего конуса через $l_2$ , то площадь боковой поверхности усеченного конуса найдется по формуле:

$S=pi*r_2*l_2-pi*r_1*l_1$

Из прямоугольных треугольников выразим каждую из образующих через радиус основания и угол наклона образующей:

$l_2=frac{r_2}{cos25}\l_1=frac{r_1}{cos25}$

Подставим и получим:

$S=pi*r_2*frac{r_2}{cos25}-pi*r_1*frac{r_1}{cos25}=frac{pi}{cos25}(r_2^2-r_1^2)frac{pi}{cos25}(12^2-8^2)=frac{80pi}{cos25}$

Приложения:

Похожие вопросы

Русский язык

2 года назад

Как вы поступите , если пожилой человек попросит вас перевести его через улицу ? Как вы поступите , если увидите , что в лифте застряли люди ? Что вы сделаете в первую очередь , если возглавите

Немецкий язык

2 года назад

напишите пожалуйста дою 20 баллов)))

Геометрия

2 года назад

помогите Две стороны прямоугольного треугольника равны: 5 см и 8 см. Найдите третью сторону треугольника. Рассмотрите все возможные случаи.

Математика

2 года назад

Привести дроби к наименьшему общему знаменателю: 4/9 и 1/7; 11/5 и 1/12; 3/84 и 1/7;

Математика

8 лет назад

Номер 1081 помогите пожалуйста

Математика

8 лет назад

сократить дробь дробь 20100

Биология

9 лет назад

НАПИШІТЬ БУДЬ ЛАСКА ДУЖЕ ВАЖЛИВОО!! Чому зараження личинками стьожкових червів викликає в людей набагато небезпечніші хвороби, ніж зараження дорослими червами?

Математика

9 лет назад

готовлюсь к огэ какое из данных ниже выражений при любых значениях n равно дроби 4n/16? с объяснением пожалуйста. варианты ответа: 1. 2^2n-2 2. 4^n-2 3. (1/4)^n 4. 4^n/2