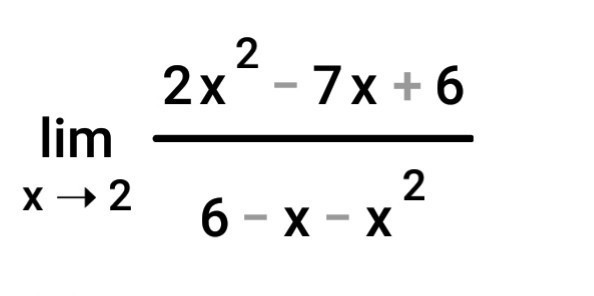найти указыные пределы

Приложения:

Ответы

Ответ дал: Artic0

Ответ:

-frac{1}{5}

Пошаговое объяснение:

Найдём корни каждого из многочленов, чтобы разложить их на множители.

$2x^2-7x+6=0,\D=49-4*6*2=1,\x_{1} =8/4=2,\x_{2}=6/4=frac{3}{2},\2x^2-7x+6=2(x-2)(x-frac{3}{2})$

$6-x-x^2=0,\x^2+x-6=0,\D=1+4*6=25,\x_{1}=frac{-1+5}{2}=2,\x_{2}=frac{-1-5}{2}=-3,\6-x-x^2=-(x-2)(x+3)$

Имеем:

$lim_{x to 2} frac{2x^2-7x+6}{6-x-x^2}= lim_{x to 2} frac {2(x-2)(x-frac {3}{2})}{-(x-2)(x+3)}=lim_{x to 2} frac {2(x- frac {3}{2})}{-(x+3)}= -frac {2*0,5}{2+3}=-frac{1}{5}$

Похожие вопросы

Қазақ тiлi

2 года назад

срочно помогите 17 жаттыгу

Русский язык

2 года назад

Заменить: "Когда люди в лесу рубят дрова, то щепки летят во все стороны" на синонимичное обобщённо-личное предложение в форме русской пословицы.

Химия

2 года назад

Составьте формулы веществ: оксид калия, оксид кальция, гидроксида магния, гидроксид лития, гидроксид хрома (III), иодид железа (III), фосфата аммония, силиката натрия.

Қазақ тiлi

2 года назад

Тындалған мәтінге өз пікіріңді білдіру үшін сұрақтарды то- лықтыр. 1. Темір неліктен бессайыс туралы әңгіме айтуға мәжбүр болды? 2. ... 3. ... . Сұрақтардың жауабын дәптерге жаз. Күрделі сөздердің

Химия

8 лет назад

1. Сколько граммов HNO3 содержится в 200 мл 40 % раствора плотностью 1250 кг/моль. Ответ: 160 г 2. Определите w% Ca(NO3)2 в растворе , полученном при смешивании 300 г 10% р-ра и 500 г 20% р-ра

Математика

8 лет назад

На поединок со змеем Кирилл Кожумяка прибежал за 6 минут со скоростью 160 метров за минуту . На обратный путь он потратил 10 минут. На сколько уменьшилась скорость Кирилла Кожумяки?

Экономика

9 лет назад

Отрасль промышленности, которая занимается производством из сырья нужных людям изделий, классифицируется как: А) обрабатывающая Б) добывающая В) топливная Г) энергетическая

Математика

9 лет назад

Тетянка почала виконувати множення х529 725 _____ 2645 1058 Яким чином записати наступний рядок, не виконуючи множення 7 на 529? СКЛАДІТЬ ПОДІБНИЙ ПРИКЛАД НА МНОЖЕННЯ!!!!!!!!