Помогите с геометрии, даю 50 баллов.
Дали на каникулы.
8 класс. Тема: Решение прямоугольных треугольников
1) На рисунке (на фото) - прямоугольный треугольник ABC (∠C = 90 °). найдите:
1. cos A
2. sin B
3. tg A
4. cos B
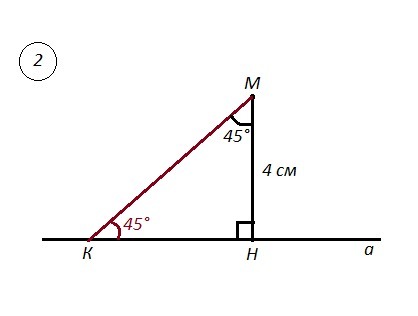
2) Точка находится на расстоянии 4 см от прямой. С этой точки до прямой проведения наклонную, что образует с прямой угол 45 °. Найдите длину наклонной и длину проекции наклонной на прямую.
3) В прямоугольном треугольнике ABC (∠C = 90 °) AC = 8 см, cos∠A = 4/5. Найдите второй катет и гипотенузу треугольника
Приложения:
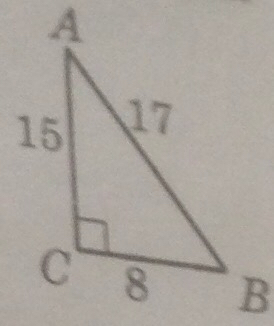
Ответы
Ответ дал:
0
Вот решение всех задач
Приложения:


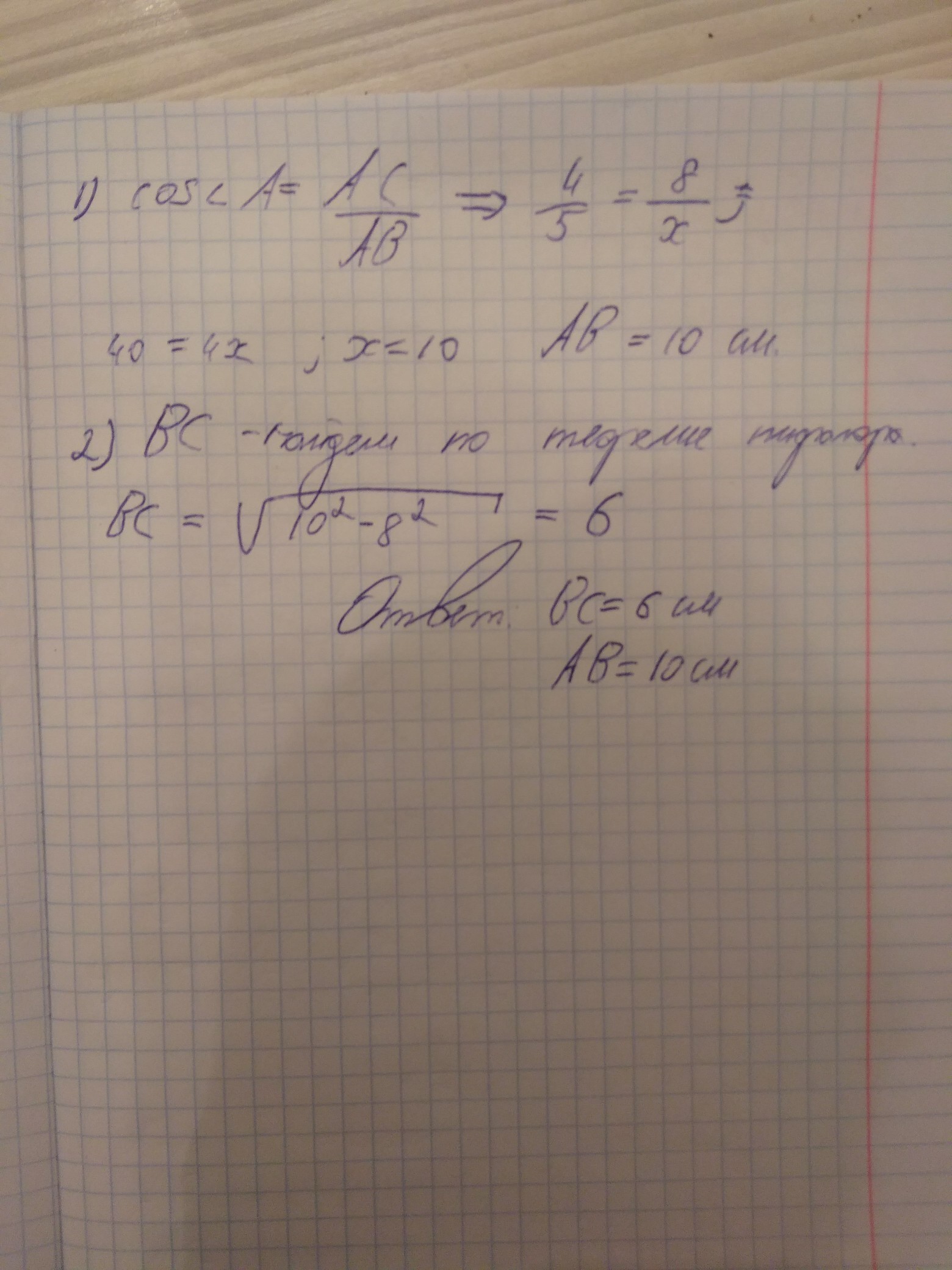
Ответ дал:
0
СПАСИБО БОЛЬШОЕ!!!!
Ответ дал:
0
1)
2) Точка М , прямая а , МН⊥ а , МН=4 см , МК - наклонная, ∠МКН=45°.
Так как ∠МКН=45°, то и ∠КМН=90°-∠МКН=45° .
Тогда ΔМКН - равнобедренный и МН=КН=4 см, то есть проекция наклонной - это КН=4 см.
Наклонная МК=√(МН²+КН²)=√(4²+4²)=√2·16=4√2 (см).
Или МК=МН:sin∠МКН=4:(√2/2)=(4·2)/√2=4√2 (см) .
3) ΔАВС , ∠С=90° , АС=8 см , cos∠А=4/5 .
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад