Ответы
Ответ дал:
0
Смотри.... .............
Приложения:
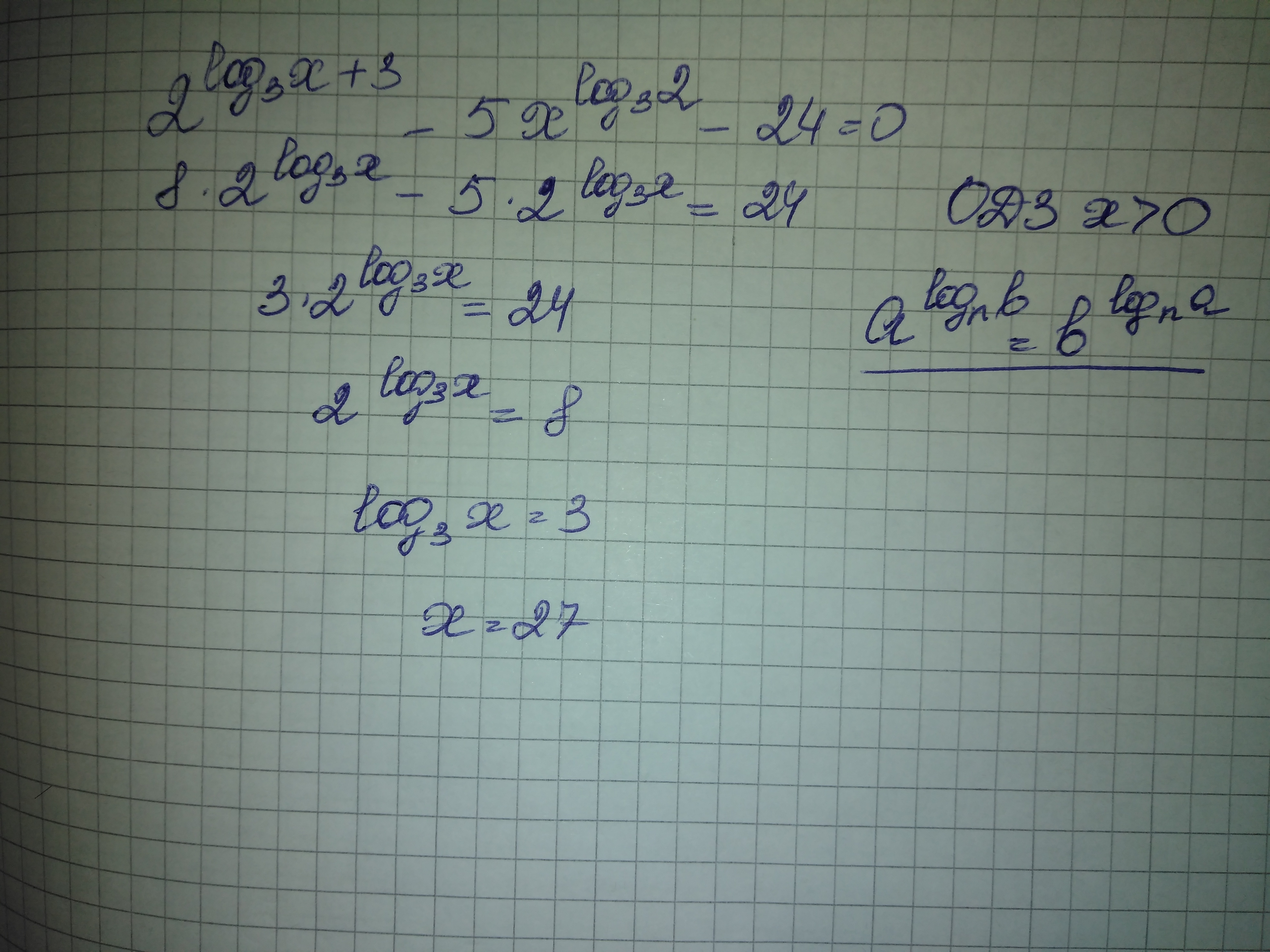
Ответ дал:
0
а разве можно просто поменять местами х и 2? не припоменаеться такой формулы тли что-то подобного
Ответ дал:
0
есть такая формула !
Ответ дал:
0
даже формулу специально написала ))
Ответ дал:
0
Эта формула достаточно легко доказывается. Прологарифмировать обе части по основанию a, затем разделить обе части на log_{n}{a}. Получим формулу приведения к новому основанию, очевидно, верную.
Ответ дал:
0
Приложения:
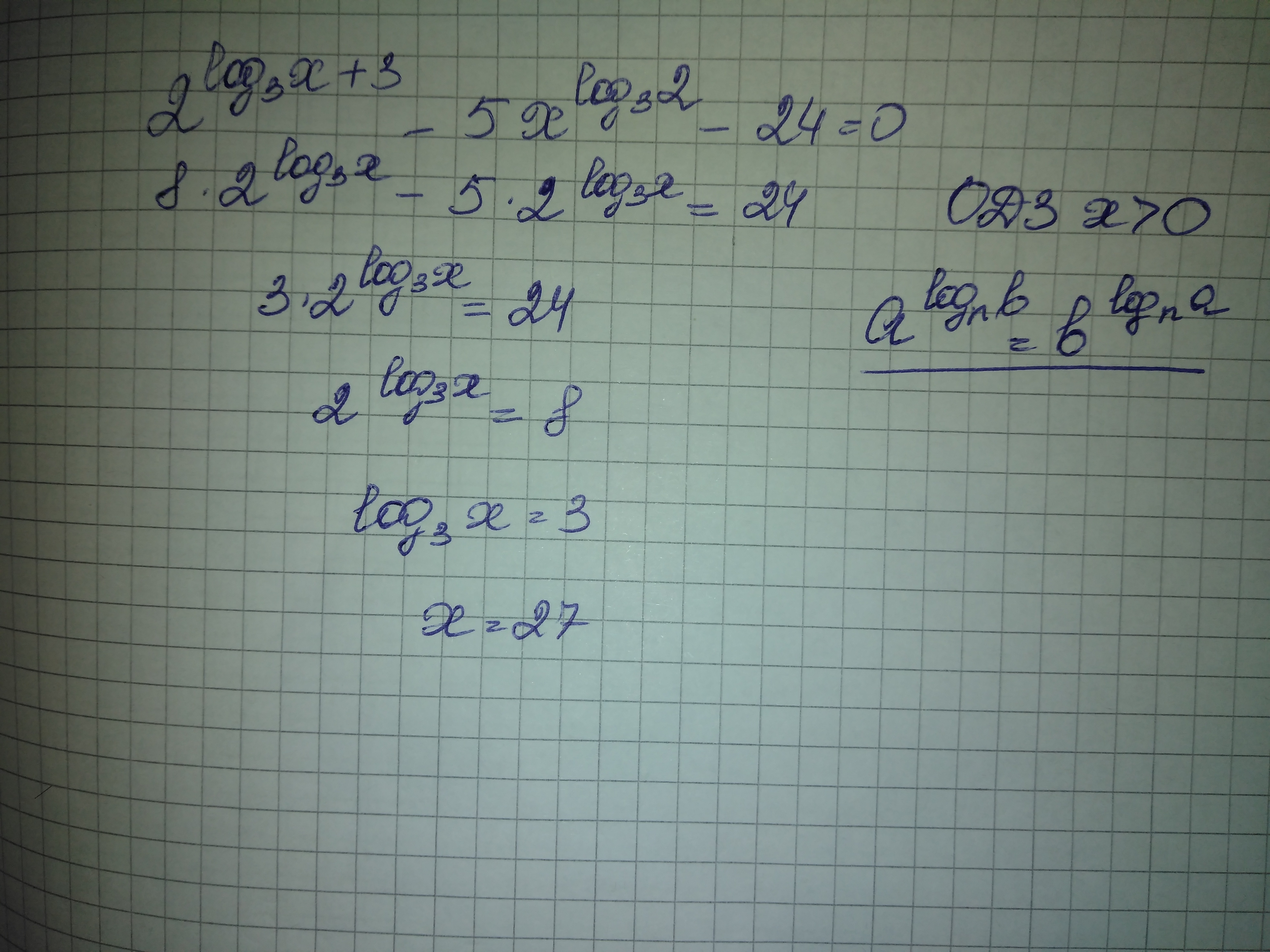
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад
