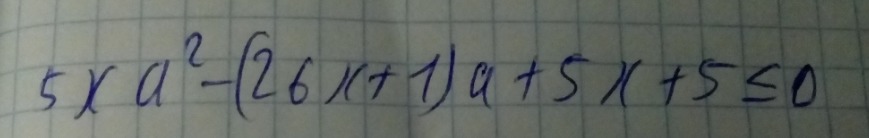Предмет: Математика
Автор: dimadima234
Вопрос задан 7 лет назад

Помогите решить параметр

Приложения:

Ответы

Ответ дал: xtoto

$5xa^2-(26x+1)a+5x+5leq 0\\5xa^2-26xa-a+5x+5leq 0\\x*(5a^2-26a+5)leq a-5\\$

Разлодим на множители $5a^2-26a+5$ и вернемся к решению неравенства:

$5a^2-26a+5=0\\D=26^2-4*5*5=(25+1)^2-4*25=25^2+2*25+1-4*25=\\=25^2-2*25+1=(25-1)^2=24^2\\a_{1,2}=frac{26pm24}{2*5}\\a_1=5 a_2=frac{1}{5}\\5a^2-26a+5=5*(a-5)*(a-frac{1}{5})=(a-5)*(5a-1)$

тогда неравенство:

$x*(5a-1)*(a-5)leq a-5$

решим следующее параметрическое уравнее:

$a*xleq b$

если $a>0$ , то $xleq frac{b}{a}\\xin(-infty; frac{b}{a}]$
если $a<0$ , то $xgeq frac{b}{a}\\xin[frac{b}{a}; +infty)$
если $a=0$ , то $0*xleq b$ : первый случай: если при этом также $bgeq 0$ , то $xin(-infty; +infty)$ второй случай: если же при этом $b<0$ , то $xnotin(-infty; +infty)$ (т.е. нету решений)

У нас:

если $5*(a-5)*(a-frac{1}{5})>0\\++++++(frac{1}{5})-------(5)+++++>a\\ain(-infty; frac{1}{5})cup(5; +infty)$ , то $x*(5a-1)*(a-5)leq a-5\\xleq frac{a-5}{(5a-1)*(a-5)}=frac{1}{a-5}\\xin(-infty; frac{1}{a-5}]$
если $5*(a-5)*(a-frac{1}{5})<0\\++++++(frac{1}{5})-------(5)+++++>a\\ain(frac{1}{5}; 5)$ , то $x*(5a-1)*(a-5)leq a-5\\xgeq frac{a-5}{(5a-1)*(a-5)}=frac{1}{a-5}\\xin[frac{1}{a-5}; +infty)$
если $5*(a-5)*(a-frac{1}{5})=0\\a=5 or a=frac{1}{5}$ первый вариант: $a=5$ , тогда $x*(5*5-1)*(5-5)leq 5-5\\x*0leq 0\\xin(-infty; +infty)$ второй вариант: $a=frac{1}{5}$ , тогда $x*(5*frac{1}{5}-1)*(frac{1}{5}-5)leq frac{1}{5}-5\\x*0leq -4.8\\xnotin(-infty; +infty)$ (т.е. решений нет)

Ответ:

при условии $ain(-infty; frac{1}{5})cup(5; +infty)$ $xin(-infty; frac{1}{a-5}]$
при условии $ain(frac{1}{5}; 5)$ $xin[frac{1}{a-5}; +infty)$
при условии $a=5$ $xin(-infty; +infty)$
при условии $a=frac{1}{5}$ $xnotin(-infty; +infty)$ (нету решений)

Также добавляю одну страницу по теме из Высоцкий "Задачи с параметрами при подготовке к ЭГЕ" 2011

Приложения:

Ответ дал: dimadima234

а нельзя ли было решить параметр через дискриминант

Ответ дал: dimadima234

тоесть с самого начала не раскрывая скобок

Ответ дал: xtoto

Т.е. предлагаешь решать относительно a (x - параметр), вместо решать относительно х (a - параметр), и после будешь формировать общий ответ (возвращаться от зависимости a(x) к зависимости x(a))? Это не оправдано, по скольку относительно x - неравенство линейно, и относительно a - квадратично. И, также, квадратическое неравенство с параметром не решаеться "через дискриминант", и как решаеться, можешь разобраться например тут: Высоцкий "Задачи с параметрами при подготовке к ЭГЕ" 2011

Похожие вопросы

Английский язык

2 года назад

Помогите пожалуйста перевести текст

Английский язык

2 года назад

THE TRANS-SIBERIAN MAINLINE “The Great Siberian Track” is a well-known name in the history of the Russian State. It was given to the unique railway that connected the European part of the country

Русский язык

2 года назад

Выбрать звуковую схему на слова замок

Биология

2 года назад