Помогите пожалуйста:)
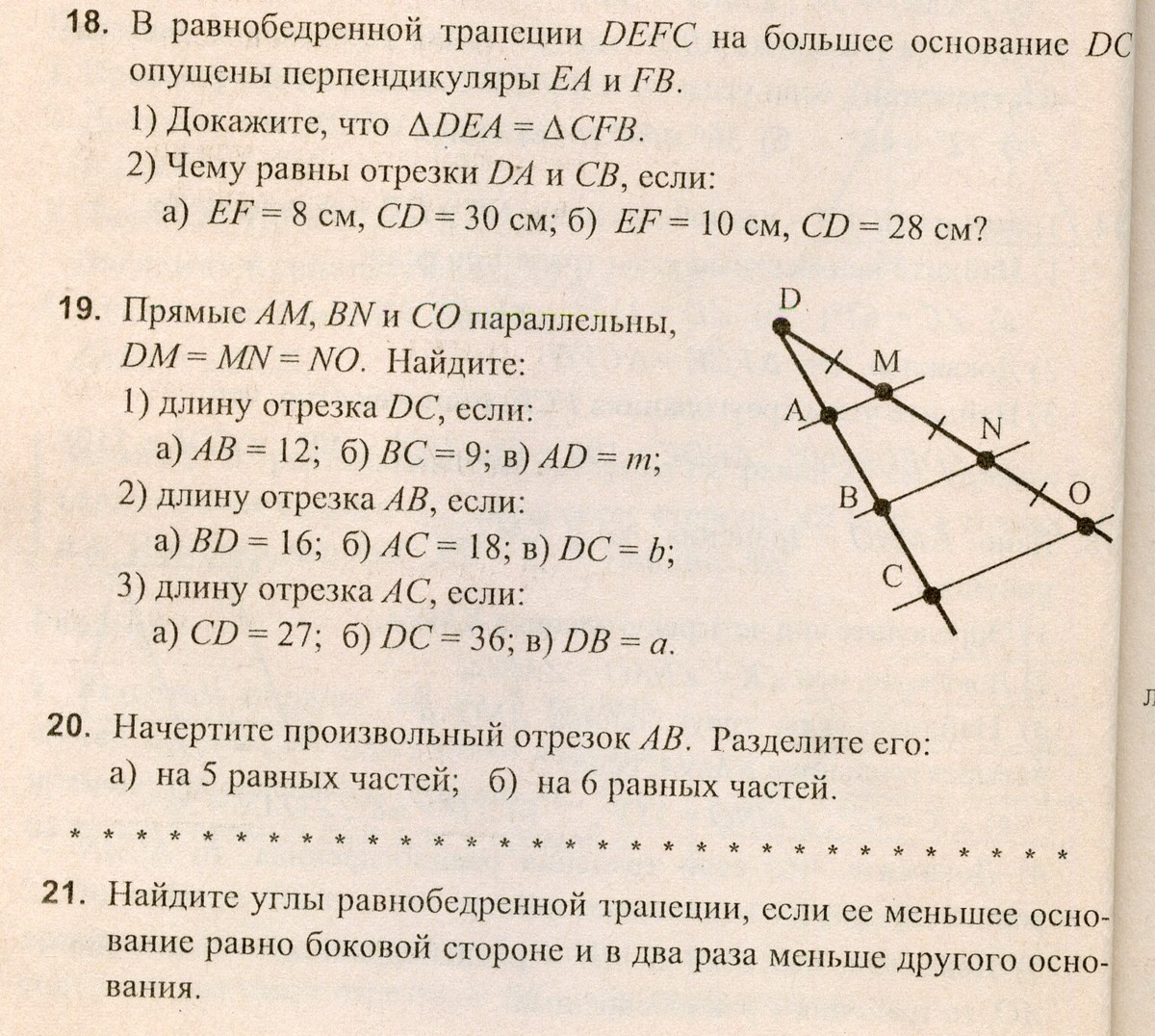
Прямые AM, BN и CO параллельны, DM = MN = NO. Найдите:
1) длину отрезка DC, если:
а) AB=12; б) BC=9см; в) AD = m
2) длину отрезка AB, если:
а) BD=16см; б) AC=18 см: в) DC=b
3) длину отрезка AC, если:
а) CD=27 см; б) DC=36см; в) DB=a
Пожалуйста завтра надо:(
2. начертите произвольный отрезок AB, Разделите его:
а) на 5 равных частей
б) на 6 равных частей
3. Найдите углы равнобедренной трапеции, если ее меньшее основание равно боковой стороне и в два раза меньше другого основания.
Приложения:
Ответы
Ответ дал:
0
20)
По теореме Фалеса так как эти отрезки равные то есть DM = MN = NO то отрезки 1)
AD=AB=BC, DC=12*3=36
AD=AB=BC, DC=3*9=27
AD=AB=BC ,DC=3m
2) 2x=16 => x=8
AB=8
2x=18=> x=9
AB=9
итд
21) Пусть боковые стороны равны х , тогда меньшее и большее соответственно равны х и 2х , выразим диагонали через боковые и основания
По теореме косинусов
![d^2=x^2+4x^2-4x^2*cosa\
d^2=2x^2+2x^2*cosa\
5x^2-4x^2cosa=2x^2+2x^2*cosa
3x^2=6x^2cosa\
cosa=frac{1}{2}\
a=60\
b=120](https://tex.z-dn.net/?f=d%5E2%3Dx%5E2%2B4x%5E2-4x%5E2%2Acosa%5C%0Ad%5E2%3D2x%5E2%2B2x%5E2%2Acosa%5C%0A5x%5E2-4x%5E2cosa%3D2x%5E2%2B2x%5E2%2Acosa%0A3x%5E2%3D6x%5E2cosa%5C+++%0A++++++cosa%3Dfrac%7B1%7D%7B2%7D%5C%0A+a%3D60%5C%0A+b%3D120 "d^2=x^2+4x^2-4x^2*cosa\
d^2=2x^2+2x^2*cosa\
5x^2-4x^2cosa=2x^2+2x^2*cosa
3x^2=6x^2cosa\
cosa=frac{1}{2}\
a=60\
b=120")
По теореме Фалеса так как эти отрезки равные то есть DM = MN = NO то отрезки 1)
AD=AB=BC, DC=12*3=36
AD=AB=BC, DC=3*9=27
AD=AB=BC ,DC=3m
2) 2x=16 => x=8
AB=8
2x=18=> x=9
AB=9
итд
21) Пусть боковые стороны равны х , тогда меньшее и большее соответственно равны х и 2х , выразим диагонали через боковые и основания
По теореме косинусов
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад