Ребят помогите пожалуйста 40 баллов дам!!!!!
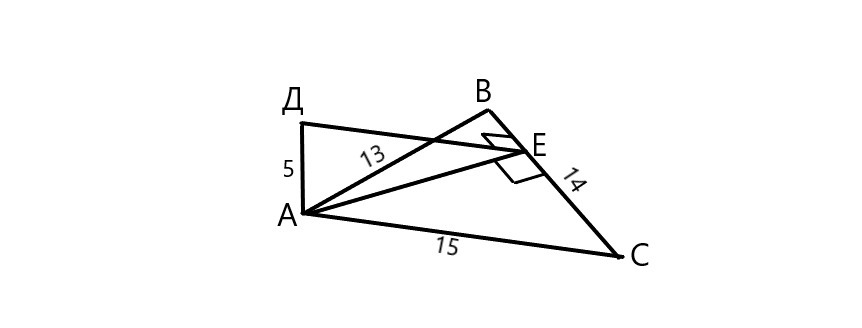
К плоскости треугольника АВС проведен перпендикуляр АД, равный 5 см. АВ=13см, ВС=14см, АС=15см. Вычислите расстояние от точки Д до стороны ВС
Ответы
Ответ дал:
0
Расстояние от точки Д до стороны ВС - перпендикуляр ДЕ. Так как АД перпендикуляр к плоскости треугольника АВС и ДЕ перпендикуляр к ВС, то АЕ тоже перпендикуляр к ВС. Следовательно АЕ высота проведенная к ВС.
Площадь треугольника АВС вычисляется по формуле Герона.
Р=13+14+15=42 см - периметр;
р=42/2=21 см - полупериметр;
S=√(p(p-a)(p-b)(p-c))=√(21(21-13)(21-14)(21-15))=√(21*8*7*6)=84 см²;
S=h*a/2 ⇒ AE=h=2S/a=2*84/14=12 см;
Треугольник АДЕ прямоугольный с катетами АЕ=12 см и АД=5 см. По т. Пифагора ДЕ=√(АЕ²+АД²)=√(12²+5²)=13 см.
Приложения:
Ответ дал:
0
Спасибо огромное!
Ответ дал:
0
пожалуйста...
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад