Алгебра 45 баллов даю

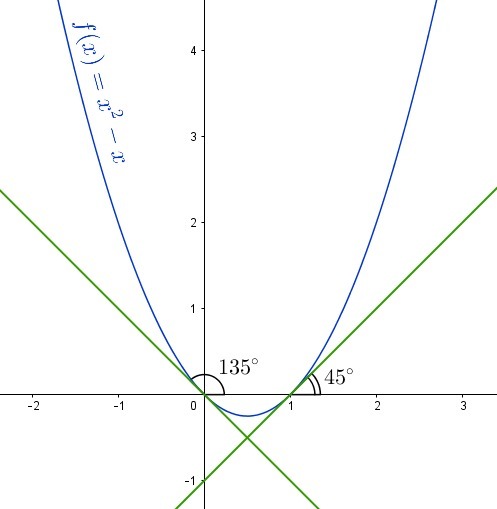
Найдите угол, под которым пересекается с осью Ox график функции f(x)=x^2-x

Найдём производную функции:

Найдём точки пересечения (то есть нули функции):

Сначала рассмотрим x=0. Найдём значение производной в этой точке:

Это значит, что угловой коэффициент касательной, проведённой в этой точке, равен −1. Обозначим искомый угол через :

Теперь рассмотрим x=1. Производная в этой точке равна

Тогда

Ответ: 135° и 45°.

***

Если будут какие-нибудь вопросы — задавайте.