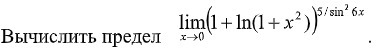Предмет: Математика
Автор: masmaks13
Вопрос задан 7 лет назад

< >

Вычислить предел(подробно)

Приложения:

Ответы

Ответ дал: Alexаndr

0

$displaystyle lim_{x to 0} (1+ln(1+x^2))^frac{5}{sin^2(6x)}=1^infty=[lim_{x to 0} (1+ln(1+x^2))^frac{1}{ln(1+x^2)}]^{frac{5ln(1+x^2)}{sin^2(6x)}}=\...=e^{displaystyle5lim_{x to 0}frac{ln(1+x^2)}{sin^2(6x)} }=e^{displaystylefrac{5}{3}lim_{x to 0}frac{x}{(1+x^2)*sin(12x)}}=\=e^{displaystylefrac{5}{3}lim_{x to 0}frac{1}{(2x*sin(12x)+12cos(12x)*(1+x^2)}}=e^{displaystylefrac{5}{36}}$

Это если раскрывать 0/0 по Лопиталю, долго,муторно да еще и возиться с производными. Пойдем другой дорогой, воспользуемся теорией о бесконечно малых величинах.

$ln(1+x^2)approx x^2 ;sin(6x)approx6x\\\displaystyle lim_{x to 0} (1+ln(1+x^2))^frac{5}{sin^2(6x)}=1^infty=[lim_{x to 0} (1+ln(1+x^2))^frac{1}{ln(1+x^2)}]^{frac{5ln(1+x^2)}{sin^2(6x)}}=\...=e^{displaystyle5lim_{x to 0}frac{ln(1+x^2)}{sin^2(6x)} }=e^{displaystyle5lim_{x to 0}frac{x^2}{36x^2}}=e^{displaystylefrac{5}{36}}$

Разница на лицо, вычислений нет, все иксы сократились и решение убавилось в масштабах.

Ответ дал: masmaks13

0

у меня 1 вопросик, что вы сделали , там где правило лопиталя, когда получилось е в степени 5/3???

Ответ дал: Alexаndr

0

Правило Лопиталя применяется если у нас неопределенность вида 0/0 ил беск/беск. Мы находим отдельно производные числителя и знаменателя.

Похожие вопросы

Русский язык

1 год назад

кто написал стихотворение и вот первый луч,скользнув по верхушкам ближайших,очень маленьких ёлочек,наконец-то заиграл на щеках у детей

Русский язык

1 год назад

зима,зимний, ... Надо чтобы корень был один и тот же ЗИМ

Биология

2 года назад

какие корни учавствуют в образовании корнеплода

Математика

2 года назад

Вычисли. (6-4/5):(1 1/3-1/4)×(2 1/3+1 2/5+1/6) Умаляю помагите у меня соч

Алгебра

8 лет назад

Дано:b1=1/9 b6=27 Найти:b2 b3 b4 b5 q неизвестно помогите пожалуйста!!!!

Музыка

8 лет назад

(1) Гайдн соната ми минор 3-я часть.(2) Моцарт соната № 11 ля мажор 1-я часть (3) Бетховен сонат № 8 ля минор 1-я часть! АНАЛИЗ

Физика

9 лет назад

Решите Пожалуйста Задачку По Физике При изменении внешнего сопротивления цепи с R1=6 Ом до R2=2 Ом КПД электрической цепи уменьшился в 2 раза. Чему равно внутреннее сопротивление источника тока?

Математика

9 лет назад

7/9и5/6 сравните дроби