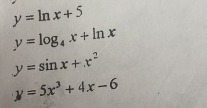Ответы
Ответ дал:
0
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Формулы:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад