докажите, что биссектрисы внутренних накрест лежащих углов, образованных двумя параллельными прямыми и секущей, параллельны, лежат на параллельных прямых.
Ответы
Ответ дал:
0
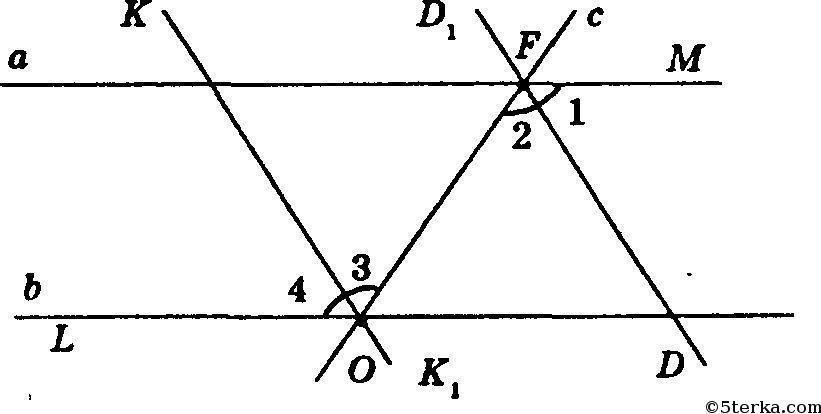
∠MFO = ∠FOL как внутренние накрест лежащие углы.
∠MFO = ∠1 + ∠2, ∠1 = ∠2, потому что FD — биссектриса.
∠FOL = ∠3 + ∠4, ∠3 = ∠4, потому что OK — биссектриса.
Таким образом, ∠1 = ∠2 = ∠3 = ∠4. Но ∠3 и ∠2 являются внутренними накрест лежащими при прямых DD1 и KK1 и секущей FO. Т.к .∠3 = ∠2, то прямые, содержащие биссектрисы, параллельны.
Приложения:
Ответ дал:
0
большое спосибо
Ответ дал:
0
можно спросить ещо, а по какому признаку по 1 или 2 или же 3 признаку?
Ответ дал:
0
пж напиши хорошо
Похожие вопросы
1 год назад
1 год назад
2 года назад
8 лет назад
8 лет назад
9 лет назад