Помогите пожалуйста.
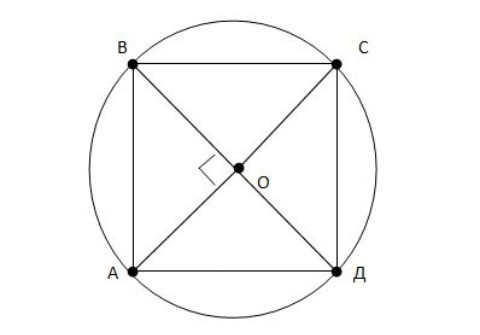
Диаметры окружности АС и ВD пересекаются под углом 90°. Длина дуги ВС равна 4П см.
а) найдите радиус данной окружности.
в) найдите длины хорд с концами в точках А, В, С, D.
И РИСУНОК обязательно.
Ответы
Ответ дал:
0
С = 4 * 4 * п = 16 * п.
По формуле длины окружности определим радиус окружности.
С = 2 * п * R = 16 * п.
R = 16 * п / 2 * п = 8 см.
Треугольники АОВ = ВСО = СОД = АОД так кА образованы пересечением диагоналей АС и ВД квадрата АВСД.
Длины хорд АВ = ВС = СД = АД и равны длине гипотенуз прямоугольных треугольников.
АВ2 = АО2 + ВО2 = 64 + 64 = 128.
АВ = ВС = СД = АД = 8 * √2 см.
Ответ: Радиус окружности равен 8 см, длины хорд равны 8 * √2 см.
По формуле длины окружности определим радиус окружности.
С = 2 * п * R = 16 * п.
R = 16 * п / 2 * п = 8 см.
Треугольники АОВ = ВСО = СОД = АОД так кА образованы пересечением диагоналей АС и ВД квадрата АВСД.
Длины хорд АВ = ВС = СД = АД и равны длине гипотенуз прямоугольных треугольников.
АВ2 = АО2 + ВО2 = 64 + 64 = 128.
АВ = ВС = СД = АД = 8 * √2 см.
Ответ: Радиус окружности равен 8 см, длины хорд равны 8 * √2 см.
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад