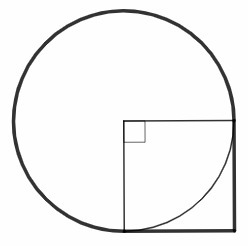
Вершина A квадрата ABCD расположена в центре круга,а вершины B и D лежат на окружности,ограничивающей этот круг.Найдите площадь фигуры,ограниченной окружностью и сторонами BC и CD квадрата,если сторона квадрата равна 3 см. Воспользуйтесь значением π=3,14.(число пи)
Ответы
Ответ дал:
0
Искомая площадь составлена из площади квадрата и 3/4 площади круга (круга с вырезанным сектором 90).
S1= r^2
S2= пr^2 - пr^2 *90°/360° =3/4 пr^2
S= S1+S2 =r^2(1 +3/4 п) =9(3,14*3/4 +1) =30,195
Приложения:
Ответ дал:
0
вероятнее всего искомая фигура не эта, а как "аппендикс" справа внизу рисунка
Ответ дал:
0
Тогда r^2(1 -п/4) =9(1 -3,14/4) =1,935
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад