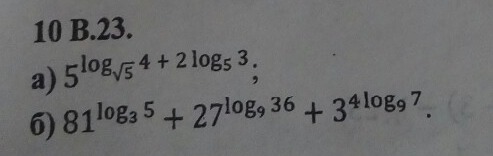Предмет: Алгебра
Автор: Saule789
Вопрос задан 7 лет назад

Помогите пожалуйста решить логарифмические выражения (15 б)

Приложения:

Ответы

Ответ дал: umnik1337288

$://2) = {3}^{ log_{3}( {5}^{4} ) } + {3}^{ log_{ {3}^{2} }( {6}^{6} ) } + {3}^{ log_{ {3}^{2} }( {7}^{4} ) } ={5}^{4}+{6}^{3}+{7}^{2}={625}+{216}+{49}={890} ://<br />1) ={5}^{log_{5}( {16} )+{log_{5} ( {9} )}}=16×9=144$

Ответ дал: umnik1337288

ща допишу, времени не хватает

Ответ дал: umnik1337288

готово

Ответ дал: Universalka

А где первое задание ?

Ответ дал: umnik1337288

ляяя

Ответ дал: umnik1337288

обнови

Ответ дал: teledima00

а)

$5^{log_{sqrt5}4+2log_53} = 5^{log_{5^{0,5}}4+2log_53} = 5^{frac{1}{0,5}log_{5}4+2log_53}= 5^{2log_54+2log_53}= \\ = 5^{2(log_54+log_53)} = 5^{2log_5{4cdot3}} = 5^{2log_512} = 5^{log_5144} = 144$

Ответ: 144

б)

$81^{log_35}+27^{log_936}+3^{4log_97}=3^{4log_35}+27^{log_{9}(9*4)}+3^{4log_{3^2}7}=\\ = 3^{log_35^4}+27^{log_{9}9+log_94}+3^{2log_37} = 5^4+27^1 cdot 27^{log_94} + 3^{log_37^2} =\\= 5^4+27cdot 3^{3log_32}+7^2 = 625 + 27cdot3^{log_32^3} + 49 = 674 + 27cdot8= 890$