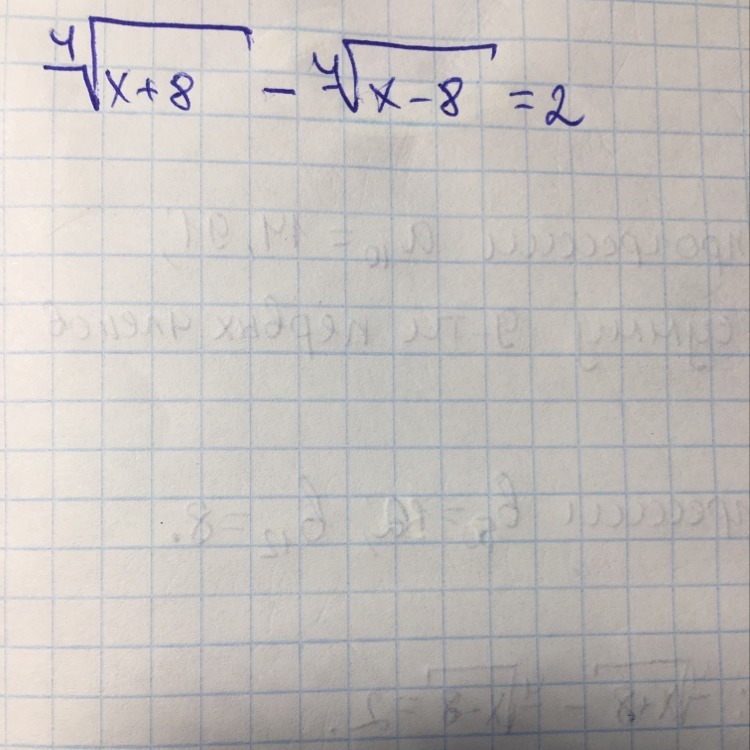• Предмет: Алгебра
  • Автор: artem180201
  • Вопрос задан 7 лет назад
< >

Срочно! Даю 25 баллов за уравнение! Только с объяснением!

Приложения:

Ответы

Ответ дал: yugolovin
0

sqrt[4]{x+8}-sqrt[4]{x-8}=2; sqrt[4]{x+8}=a; sqrt[4]{x-8}=b; left { {a-b=2} atop {a^4-b^4=16}} right.; left { {{a-b=2} atop {(a^2-b^2)(a^2+b^2)=16}} right.;

left { {{a-b=2} atop {(a-b)(a+b)(a^2+b^2)=16}} right.; left { {{a=b+2} atop {2(2b+2)(2b^2+4b+4)=16}} right.; left { {{a=b+2} atop {(b+1)((b+1)^2+1)=2}} right..

Решим второе уравнение. Замена b+1=c; c(c^2+1)=2; c^3+c-2=0; (c^3-1)+(c-1)=0; (c-1)(c^2+c+1)+(c-1)=0;

(c-1)(c^2+c+2)=0. Поскольку дискриминант квадратного трехчлена во второй скобке отрицателен, эта скобка в ноль не обращается. Поэтому единственное решение c=1; b=0; x=8.

Проверка: 2-0=0 - верно.

Ответ: 8

Замечание. Можно было кубическое уравнение относительно c не решать, а угадать c=1, после чего сослаться на монотонность левой части.

Ответ дал: artem180201
0
А ответ правильный))
Ответ дал: artem180201
0
Поэтому лайк
Ответ дал: yugolovin
0
В условии ясно написано, что корень извлекается из x+8 и x-8.
Ответ дал: artem180201
0
У вас неправильно записано. Нету ни одного знака «+»
Ответ дал: yugolovin
0
Первый корень - это корень из (x плюс 8). Если бы это был знак умножения, крестик был бы повернут на 45 градусов.
Похожие вопросы
Английский язык
2 года назад
Напиши цифры от 1 до 12
Русский язык
2 года назад
дано начало,придумайте продолжение этому рассказу (сочинение) Помогите плиз закончить текст!!! В глубине одного сада росло необычное дерево. Кто угодно мог встать под него и пожелать чего - нибудь, и
Русский язык
2 года назад
природы Прочитай текст. Выбери из списка подходящий заголовок для каждой части текста. Пришла весна (Л.Н. Толстой) 1. Пришла весна. По мокрым улицам журчали торопливые ручьи. Все стало ярче, чем
Математика
2 года назад
Раскрытие скобок. Коэффициент. Подобные слагаемые. Приведите подобных слагаемых. Урок 2 Найди недостающие коэффициенты. Заполни пропуски. ПЖ ПОМОГИТЕ! ​
История
8 лет назад
да якой дынастыі належаў жыгімонт 2 аўгуст?
Алгебра
8 лет назад
В уравнении x2+px+100=0, один из корней x1=5. Найди значение p и другой корень уравнения. Ответ: x2=;p= Помогите срочно пожалуйста!
История
9 лет назад
Срочно! Как называется наука,изучающая предметы и вещи, использовавшимися людьми и быту?
Математика
9 лет назад
у данилы в рюкзаке 4 карандаша 2 красных и 2 синих .костя хотел вынуть из портфеля красный карандаш. сколько он должен взять карандашей что бы среди них обязательно был красный?