• Предмет: Алгебра
  • Автор: CharlizLebedeva
  • Вопрос задан 7 лет назад
< >

Помогите пожалуйста решить одно логарифмическое выражение! Даю 50 баллов! Задание на фото. Спасибо большое за помощь!

Приложения:

Ответы

Ответ дал: Universalka
0

9^{log_{3}(1+0,5+0,25+...) }

1 + 0,5 + 0,25 + ... - это бесконечно убывающая геометрическая прогрессия, в которой :

b₁ = 1       b₂ = 0,5

q = b₂ : b₁ = 0,5 : 1 = 0,5

Найдём сумму членов этой прогрессии :

S=frac{b_{1} }{1-q}=frac{1}{1-0,5}=frac{1}{0,5}=2\\9^{log_{3} 2}=(3^{2})^{log_{3}2 }=(3^{log_{3}2 })^{2}=2^{2}=4



Ответ дал: CharlizLebedeva
0
Спасибо огромное!
Ответ дал: CharlizLebedeva
0
А не могли бы Вы помочь с ещё одним логарифмическим выражением?
Ответ дал: CharlizLebedeva
0
Сейчас задам вопрос
Ответ дал: CharlizLebedeva
0
Пожалуйста помогите
Ответ дал: valenivan
0

Ответ 4. Решение задания приложено

Приложения:
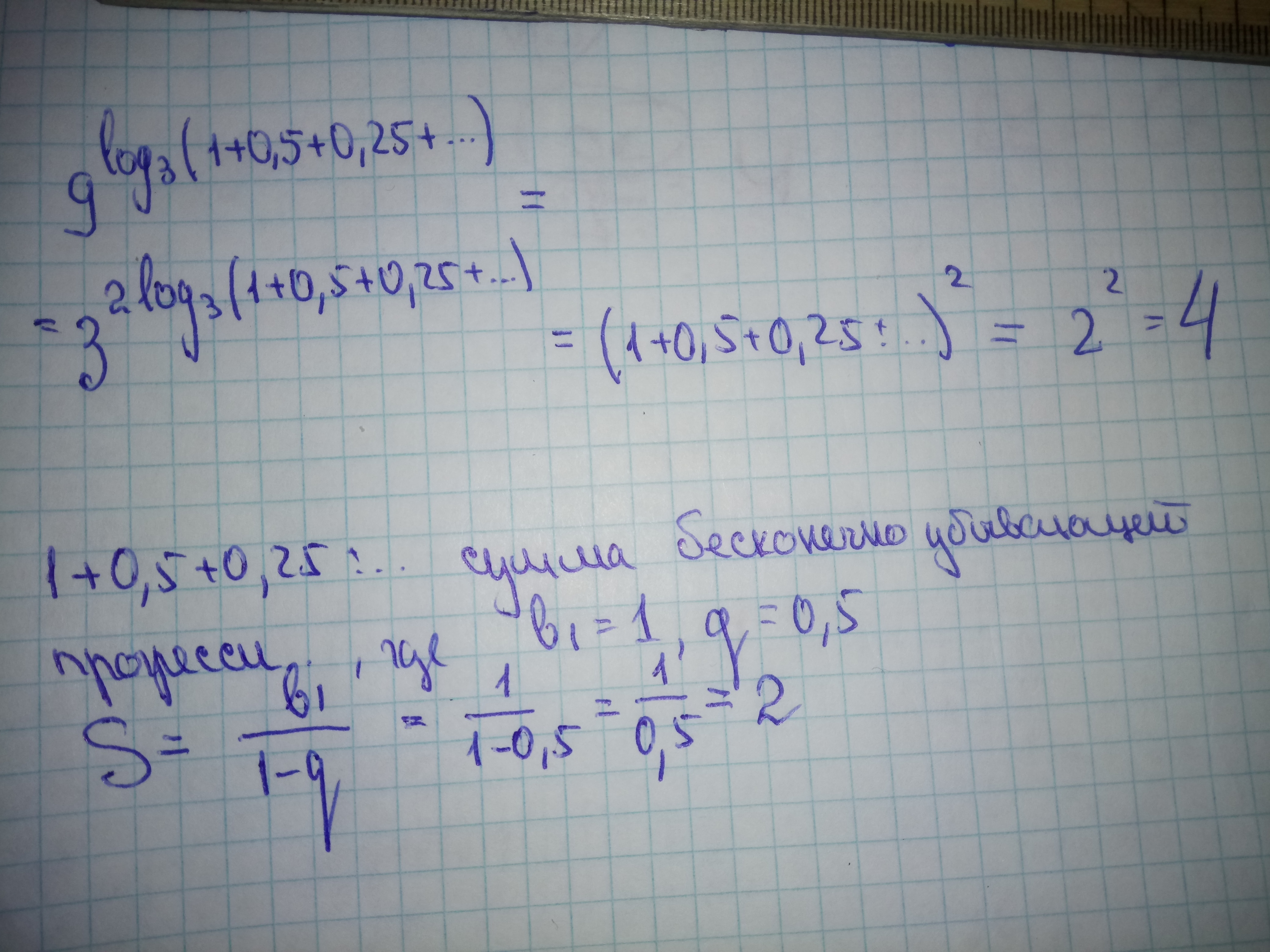
Ответ дал: CharlizLebedeva
0
Спасибо большое!
Ответ дал: CharlizLebedeva
0
А не могли бы Вы помочь с ещё одним логарифмическим выражением?
Ответ дал: CharlizLebedeva
0
Сейчас задам вопрос
Ответ дал: CharlizLebedeva
0
Пожалуйста помогите
Похожие вопросы
Английский язык
2 года назад
помогите 1 упражнение
Русский язык
2 года назад
кой частью речи является слово "неуклюже"
Математика
2 года назад
Печь выпекает 150 батонов за 3 минуты. Сколько батонов выпечет эта печь за 5 минут? ПЛИС ПОМОГИТЕ ЗАДАЧА ПРОСТАЯ С КРАТКОЙ ЗАПИСЬЮ ​
Английский язык
2 года назад
Complete the dialogue witch the correct phrase​
Математика
8 лет назад
Из двух пунктов навстречу друг другу одновременно отправились пешеход и велосипедист. К моменту встречи пройденные ими расстояния относились 1:4. Укажи расстояние между пунктами, если известно, что
История
8 лет назад
используя памятки 3,5,6, придмайте рассказ о олимпийских играх от лица участникаилисудьи. помогите плиииз ))))))!!!!!!!!
Математика
9 лет назад
Помогите пожалуйста сделать, зад. На фотке
Химия
9 лет назад
Как называются C5H8 и С6Н10?