Предмет: Алгебра
Автор: gorbacheva02
Вопрос задан 7 лет назад

< >

cos^2x – sin^2x = sinx – cosx

Ответы

Ответ дал: NeZeRAvix

0

$sf cos^2x-sin^2x=sinx-cosx \ (cosx-sinx)(cosx+sinx)+(cosx-sinx)=0 \ (cosx-sinx)(cosx+sinx+1)=0 \ \ cosx-sinx=0 \ sinx=cosx \ tgx=1 \ boxed{sf x=dfrac{pi}{4}+pi k } \ \ \ cosx+sinx+1=0$

Применим универсальную тригонометрическую подстановку

$sf dfrac{1-t^2}{1+t^2}+dfrac{2t}{1+t^2}+1=0 \ 1-t^2+2t+1+t^2=0 \ t=-1 \ \ tgleft(dfrac{x}{2} right)=-1 \ dfrac{x}{2}=-dfrac{pi}{4}+pi k\ boxed{sf x=-dfrac{pi}{2}+2pi k}$

При этом cos(π)+sin(π)+1=-1+0+1=0, значит нужно добавить решение

$boxed{sf x=pi+2 pi k}$

Ответ: $left [ begin{array}{I} sf x=dfrac{pi}{4}+pi k \ sf x=pi+2 pi k\ sf x=-dfrac{pi}{2}+2pi k end{array}; sf k in mathbb{Z}$

Ответ дал: antonovm

0

Решение : ////////////////////////////////////

Приложения:

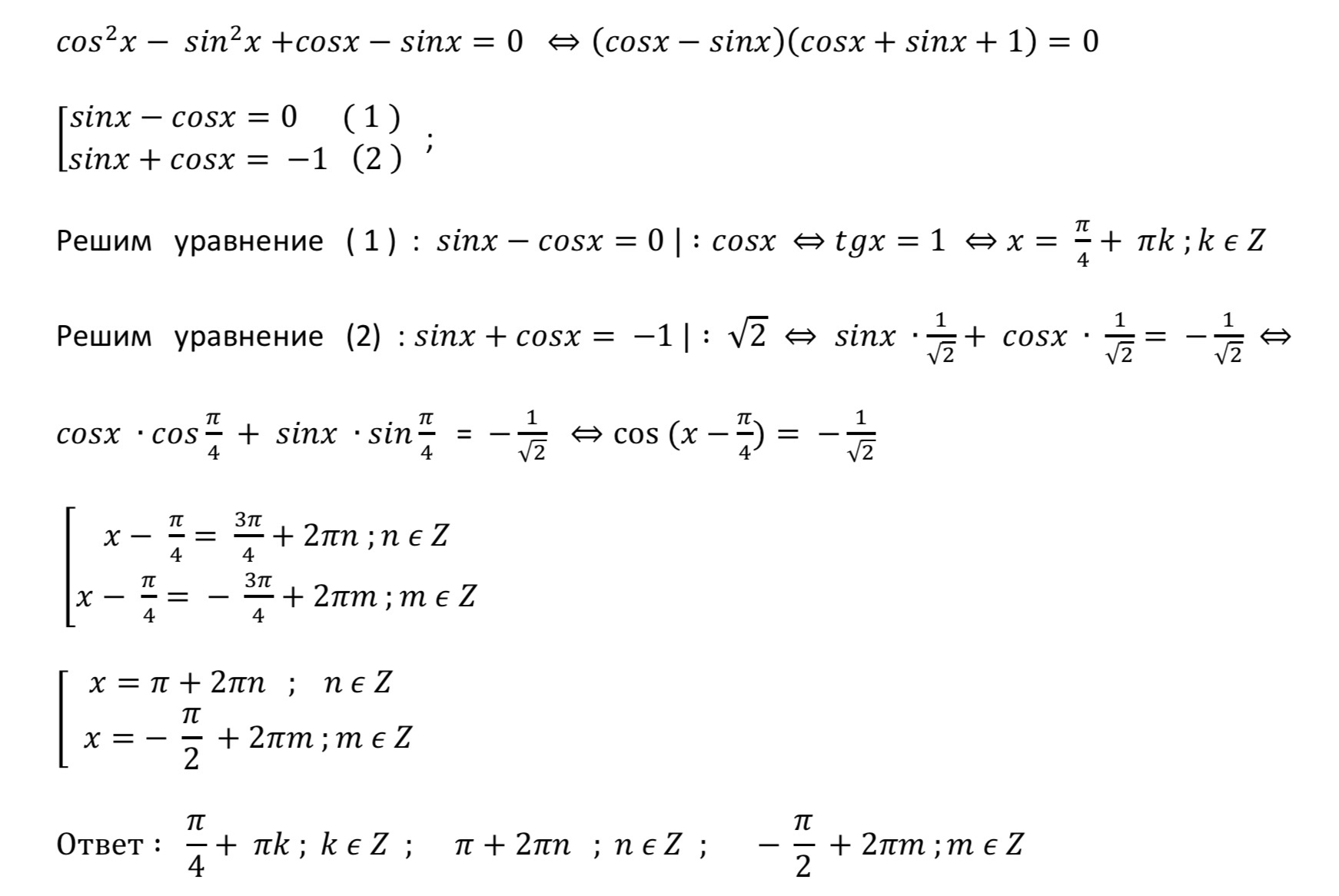
Похожие вопросы

Английский язык

2 года назад

Друзья,помогите с английским.5 задание.Довольно сложно ,как для меня.

Українська мова

2 года назад

Скласти речення зі словом Власності

Геометрия

2 года назад

18°17'+11°43' , 98°17'+11°43'

Математика

2 года назад

помогите найти периметр квадрата,если сторона равна 16 см

Математика

8 лет назад

СРОЧНО!!!ИЗВЕСТНО ЧТО КОНЦЕРТЫ КРОТА ИДУТ БОЛЬШЕ ЧАСА НО МЕНЬШЕ ЧАСА И 15 МИНУТ СКОЛЬКО БЫ МОГ ИДТИ ЕГО КОНЦЕРТ? ОТВЕТЫ:80МИН 76 МИН 66 МИН

Математика

8 лет назад

Даю 100 баллов. 5 и 6.

География

9 лет назад

Какая из перечисленных эпох складчатости находилась в протерозое? альпийская байкальская герцинская каледонская

Математика

9 лет назад

Выполните действия:( 2/3+0,6)*3/19-0,15 Помогите плиз(