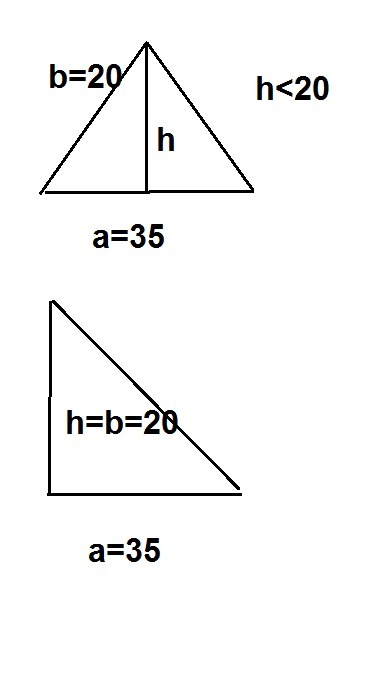А) если сторону треугольника равны 20 и 35 см. Какое максимальное значение может принимать его площадь
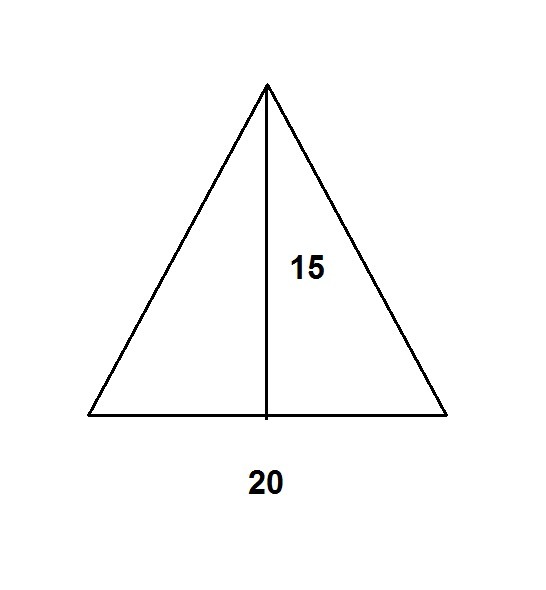
В) Найдите площадь прямоугольного треугольника и высоту проведенную к гипотенузе если его катеты равны 15 и 20 см. Постройте равнобедренный треугольник площадь которого равна площади этого треугольника
Ответы
Ответ:
другой вариант первой задачи пусть основание =35 а боковая сторона= 20
боковая сторона является наклонной к основанию а высота перпендикуляром наклонная больше перпендикуляра ⇒ высота < боковой стороны. максимальная высота и соответственно максимальная площадь будет если высота совпадет с боковой стороной это будет когда треугольник прямоугольный
S=ab/2=35*20/2=350 кв.см
площадь треугольника = a*h/2 будет максимальной если высота будет равна боковой стороне см. рисунок
Пошаговое объяснение:
А) s=(1/2)absinc
максимальное значение sinС=1 ⇒ угол С=90°
Smax=(1/2)*20*35=10*35=350 cм²
B) S=ab/2=15*20/2=15*10=150 cм²
по теореме Пифагора с²=a²+b²=15²+20²=225+400=625
c=√625=25
S=ab/2=ch/2 ⇒ ab=ch
h=ab/c=15*20/25= 12 см
чтобы построить равнобедренный треуг. площадь которого =150
надо подобрать основание и высоту чтобы S= ah/2=150
ah=2*150=300 например a=20 h=15