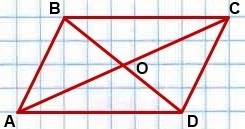
При каких условиях можно утверждать, что выпуклый четырёхугольник ABCD, диагонали которого пересекаются в точке O, является параллелограммом?
1. AB = CD, а стороны BC и AD параллельны
2. AO=OC, а стороны AB и CD параллельны
3. AO=OC и AD = BC
4. AO = OC и ∠ABC=∠ADC
Ответы
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
AB ∥ CD, AD ∥ BC.
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
Например, это могут быть пары треугольников
1) ABC и CDA,
2) BCD и DAB,
3) AOD и COB,
4) AOB и COD.
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
Для этого можно доказать равенство одной из тех же пар треугольников.
4) Четырехугольник — параллелограмм, если у него противоположные стороны попарно равны.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.