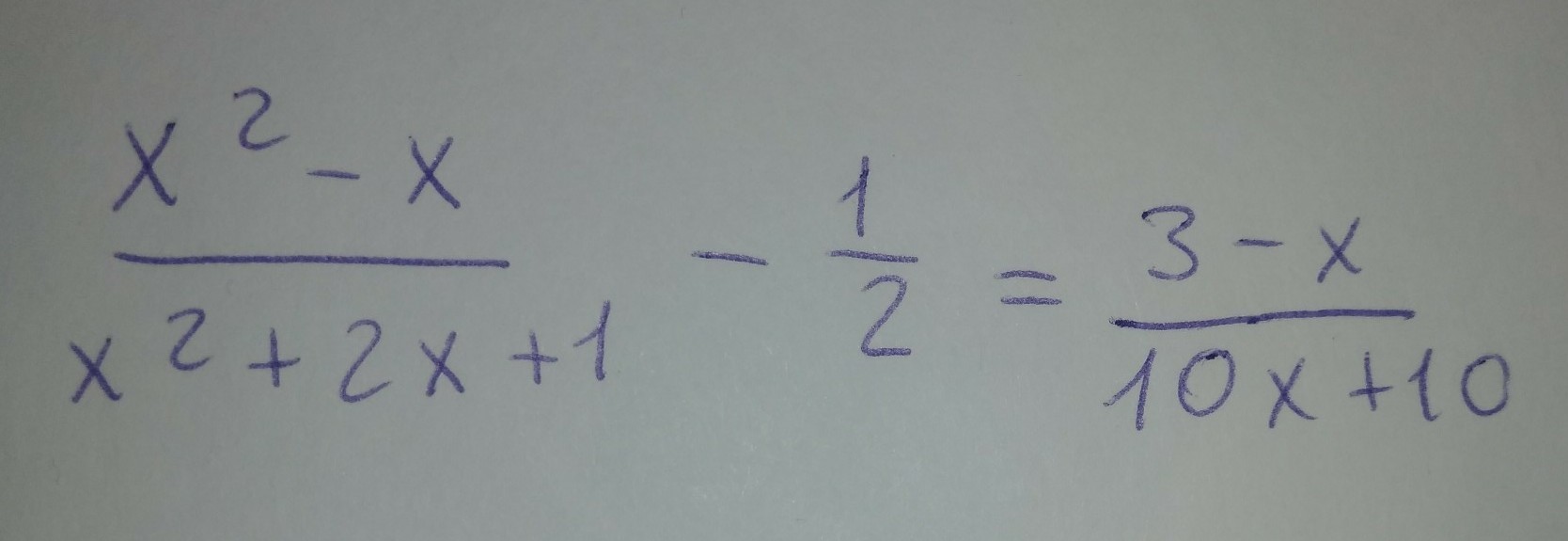Укажите все целые решения дробно рационального уравнения.

Приложения:

Ответы

Ответ дал: zinaidazina

$frac{x^2-x}{x^2+2x+1}-frac{1}{2}=frac{3-x}{10x+10}$

$frac{x^2-x}{(x+1)^2}-frac{1}{2}=frac{3-x}{10(x+1)}$

$frac{x^2-x}{(x+1)^2}-frac{1}{2}-frac{3-x}{10(x+1)}=0$

$frac{10*(x^2-x)-1*5*(x^2+2x+1)-(3-x)(x+1)}{10(x+1)^2}=0$

ОДЗ: x≠ -1

$10*(x^2-x)-1*5*(x^2+2x+1)-(3-x)(x+1)=0$

$10x^2-10x-5x^2-10x-5-3x+x^2-3+x=0$

$6x^2-22x-8=0$

Разделим обе части уравнения на 2 и получим:

$3x^2-11x-4=0$

$D=121-4*3*(-4)=121+48=169=13^2$

$x_1=frac{11-13}{2*3}=frac{-2}{6}=-frac{1}{3}$

$x_2=frac{11+13}{2*3}=frac{24}{6}=4$

Оба корня удовлетворяют ОДЗ, они не равны -1, но по условию решение должно быть целым, поэтому ответ: х = 4.

Похожие вопросы

Английский язык

1 год назад

Русский язык

1 год назад

Математика

2 года назад

Английский язык

2 года назад

Алгебра

8 лет назад

Физика

8 лет назад

Музыка

9 лет назад

Физика

9 лет назад