Предмет: Алгебра
Автор: Izimgalievaainelek
Вопрос задан 7 лет назад

у=3х^2+4х-1
условия :
а )Запишите координаты вершины параболы
Б )Определите в каких четвертях находится график функции
В )Запишите ось симметрии параболы
Г )Найдите точки пересечения с осями координат
Д ) постройте график функции

y=-x^2+5x-4
a ) Найдите решение функции
F (2) , f (-1)

Ответы

Ответ дал: WhatYouNeed

$y=3x^2+4x-1\y=3(x^2+2*2x/3+(2/3)^2-(2/3)^2)-1\y=3(x+2/3)^2-7/3$

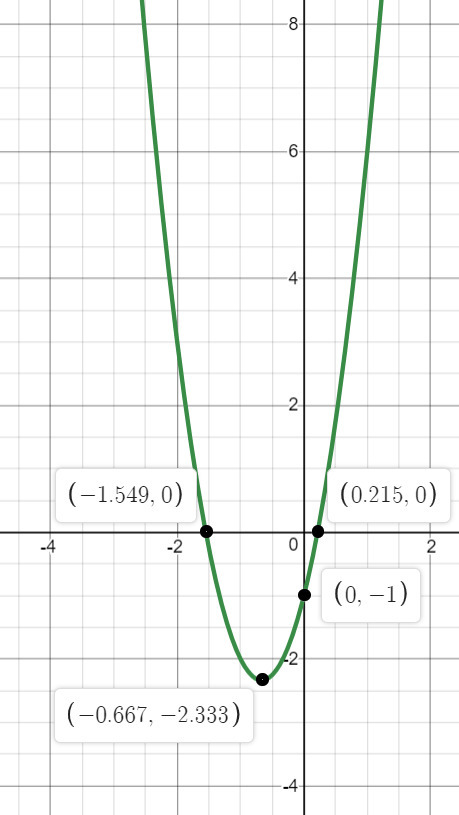
а) координаты вершины: (-2/3;-7/3)

б) Область определения все числа, значит функция точно в 1 и 2 четверти, область значения [-7/3;+∞) и у(0)=-1, значит во всех четвертях, но больше всего в 1 и 2.

в) Ось симметрии x=-2/3

г) Точки пересечения у осями: $y(0)=3*0^2+4*0-1=-1\x(0)=бsqrt{frac{7}{9} } -2/3=frac{бsqrt{7}-2}{3}$

д) У нас есть всё чтобы построить график, строим его.

$y=-x^2+5x-4$

а) Вообще функции F, f нам неизвестны, известно только функция у, так что это не совсем корректно. Для нахождение значений, необходимо поставить значение вместо переменной.

$F(2)=-(2)^2+5*2-4=10-8=2\f(-1)=-(-1)^2-5*1-4=-6-4=-10$