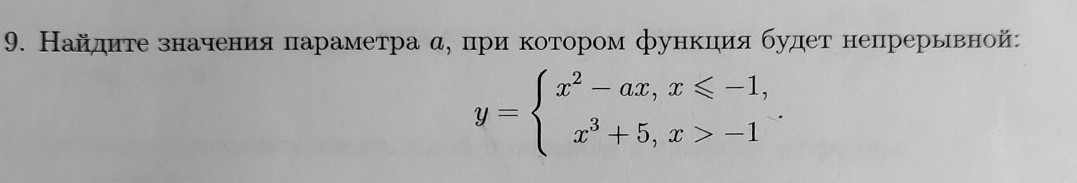решите пожалуйста;)​

Для заданной кусочной функции, чтобы она была непрерывной, надо приравнять значения функции в точке перемены, то есть в точке х = -1.

у(-1) = 1 + а,

у(-1) = -1 + 5 = 4

Приравняем: 1 + а = 4, отсюда а = 4 - 1 = 3.

Ответ: а = 3.

Тк  обе функции неперерывны  и возрастают на всей  числовой оси,то обрыв может быть только в точке их разделения  xп=-1

Чтобы функция была непрерывной(не имела разрыва),необходимо чтобы парабола имела значение в точке перехода 2-x функций:

то  есть в xп=-1 .  

Найдем значение ординаты переходной точки:

yп=xп^3+5=(-1)^3+5=4

тогда  подставим  эту координату в нашу параболу:

4=(-1)^2-a*(-1)

4=1+a

a=3