Найдите площадь равнобедренного треугольника Боковая сторона которого равна 25 см а высота 20.​

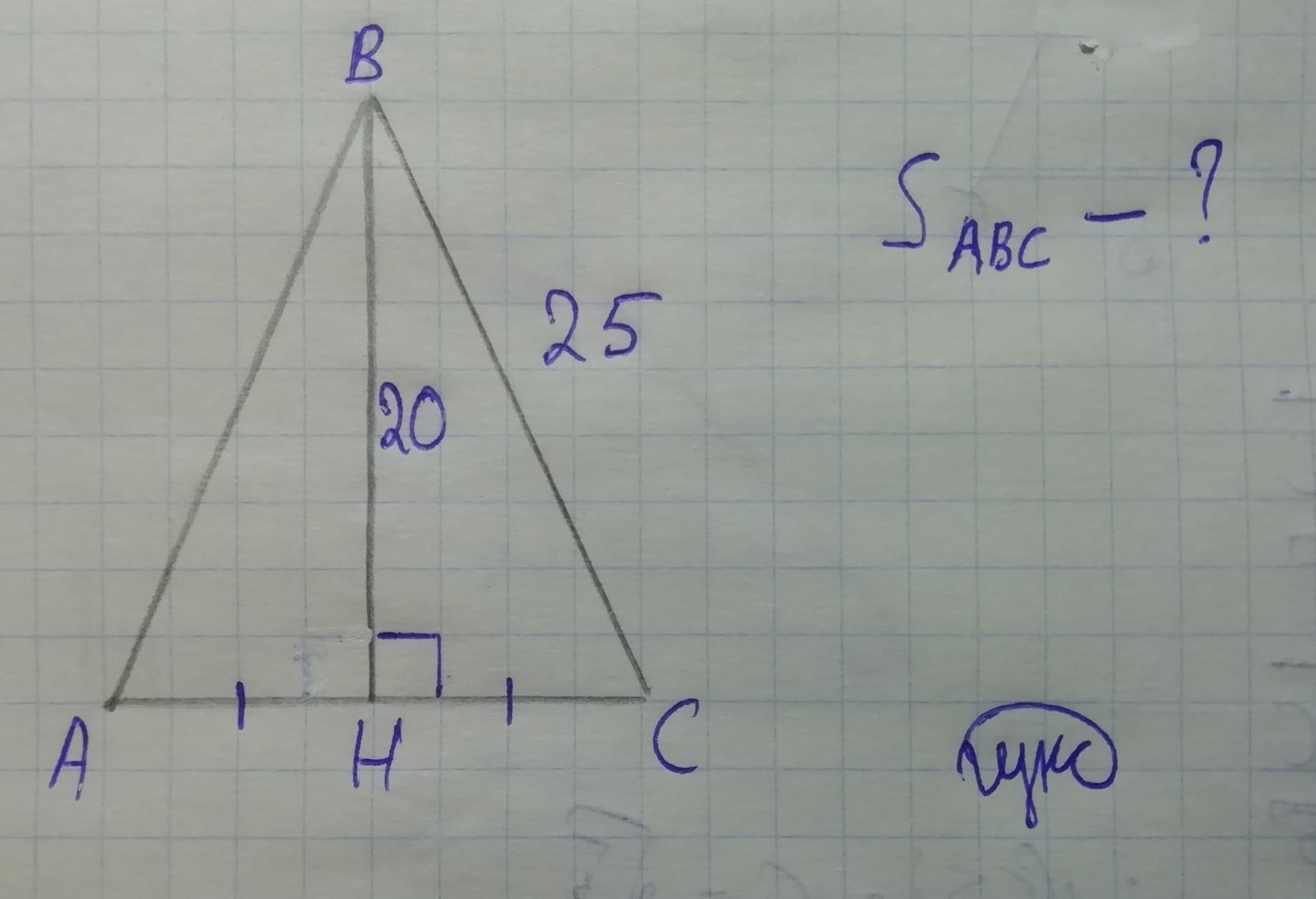
По теореме Пифагора находим основание

АН²=25²-20²=√225

АН=15 - это половина основания тогда АС=2АН=30

площадь равна 0.5аh

0.5*30*20=300

Рассмотрим ΔHBC - прямоугольный: BC = 25 см, BH = 20 см, HC - ?

По теореме Пифагора



AC = 2HC = 15 * 2 = 30 см (высота в равнобедренном треугольнике, проведенная к основанию, является его медианой)

Формула площади (S) треугольника:



где a - основание, h - высота, проведенная к основанию.



Ответ: S = 300 см.