• Предмет: Алгебра
  • Автор: n1523321
  • Вопрос задан 7 лет назад
< >

Найти промежутки убывания и возрастания : y=√x²+8x
(Все уравнение под корнем)

Ответы

Ответ дал: WhatYouNeed
0

y=sqrt{x^2+8x}\y'=frac{(x^2+8x)'}{2sqrt{x^2+8x}}=\frac{2x*1+8}{2sqrt{x^2+8x}}=frac{x+4}{sqrt{x^2+8x}};\x^2+8xgeq0=&gt;left[begin{array}{ccc}xleq-8\xgeq0\end{array}

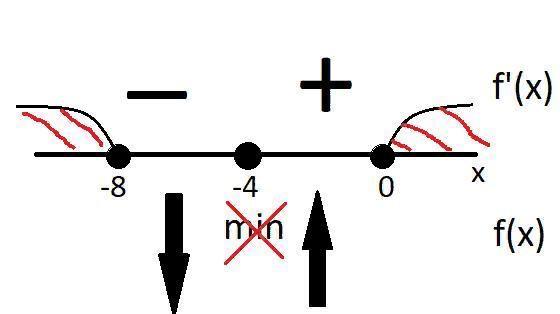
Когда производная положительная функция возрастает, когда отрицательная - убывает.

Ответ: убывает - (-∞;-8]

           возрастает - [0;+∞)

Приложения:
Ответ дал: Ivanov2017
0
-8 и 0 должны быть включены в ответ, потому что сама функция при этих значениях определена, хотя производная и не определена при этих значениях.
Ответ дал: Ivanov2017
0
Ответ: убывает - (-∞;-8] возрастает - [0;+∞)
Ответ дал: Ivanov2017
0
при x-> -8 (слева x<8) производная y' -> -∞ (отрицательная)
Ответ дал: Ivanov2017
0
при x-> 0 (справа x>0) производная y' -> +∞ (положительная)
Ответ дал: Ivanov2017
0
поправка: при x-> -8 (слева x<-8) производная y' -> -∞ (отрицательная)
Похожие вопросы
Русский язык
1 год назад
Помогите!!!!!!! Даю 50 баллов
Русский язык
1 год назад
Помогите пож срочно хотябы что-то пж или обясните как сделать лучше сразу ответ ну помогите пж
Биология
2 года назад
1. Как называется процесс обмена газов между атмосферным воздухом и кровью? а) Легочное дыхание б) Тканевое дыхание в) Дыхание г) Транспорт газов кровью 2. Как называется процесс обмена
Русский язык
2 года назад
ПОМОГИТЕ ПОЖАЛУЙСТА СЕЙЧАС ЖЕ УМОЛЯЮ ВАААААС
Алгебра
8 лет назад
НЕ ИЗ ИНТЕРЕСНЕТА ПЛЭЗ токарь должен был обработать 80 деталей к определенному сроку. он обработал в час на 2 детали больше, чем планировал, и уже за 1 час до срока обработал на 4 детали больше.
Биология
8 лет назад
помогите прошу это очень срочно...
Математика
9 лет назад
Найти 4,5 % от 20,4 Заранее спасибо!
География
9 лет назад
Как образуется течение Эль-Нинно?