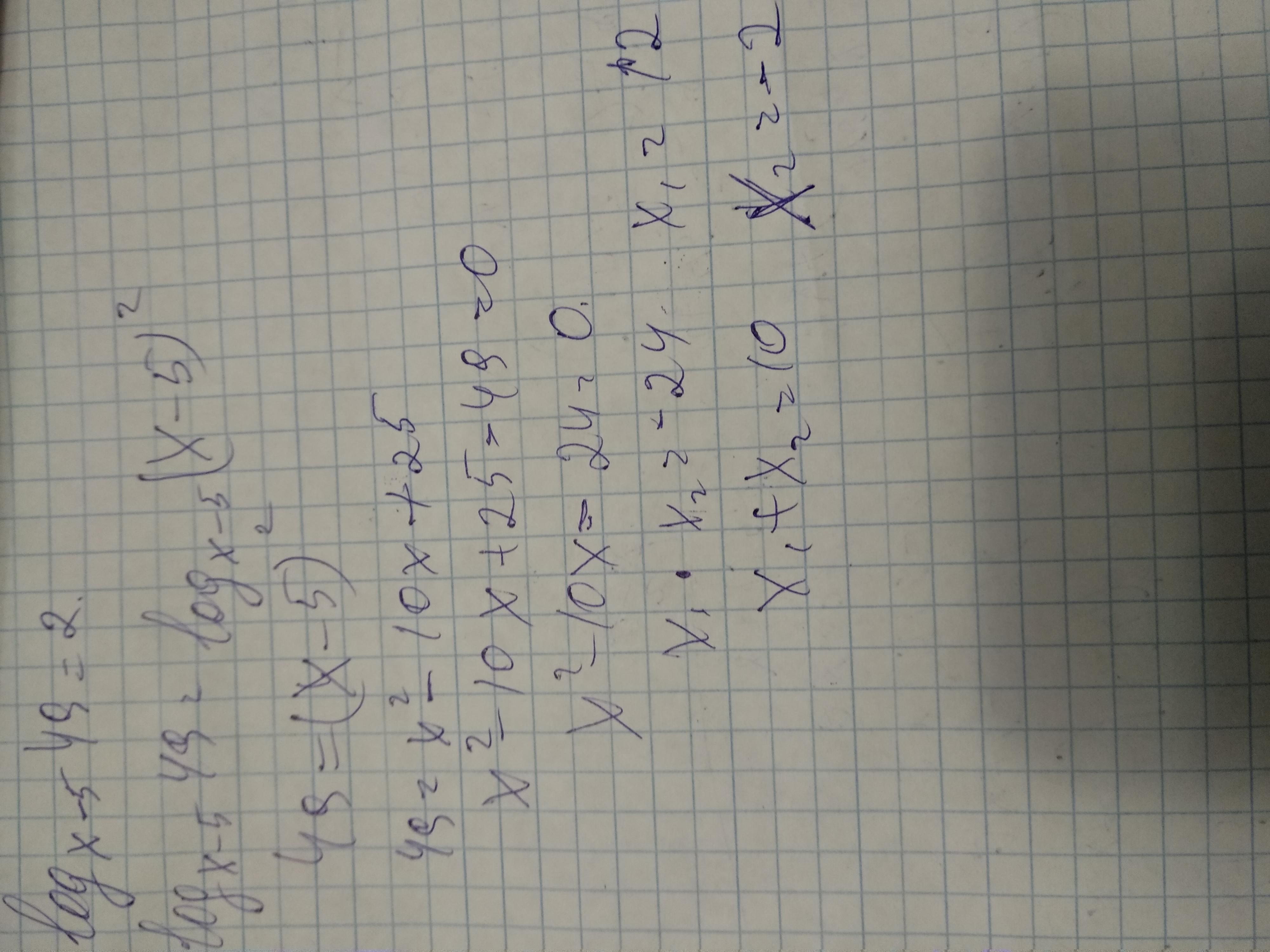Предмет: Алгебра
Автор: KoralinaJ
Вопрос задан 7 лет назад

< >

Как решить ОДЗ? Объясните, плес)

Приложения:

Ответы

Ответ дал: NNNLLL54

0

ОДЗ: основание log должно быть >0 и не 1, а агумент >0, то есть

$log_{x-5}49=log_{x-5}(x-5)^2\\ODZ:; ; left { {{x-5>0; ,; x-5ne 1} atop {(x-5)^2>0}} right. ; left { {{x>5; ,; xne 6} atop {x-5ne 0}} right. ; left { {{x>5; ,; xne 6} atop {xne 5}} right. ; ; to \\underline {; xin (5,6)cup (6,+infty ); }\\49=(x-5)^2\\x^2-10x-24=0\\x_1=-2notin ODZ; ; ; ,; ; x_2=12in ODZ\\underline {Otvet:; ; x=12; .}$

Ответ дал: KoralinaJ

0

Откуда 6?

Похожие вопросы

Русский язык

2 года назад

Сочинение рассуждение на тему "Надежда". Заранее спасибо.

Технология

2 года назад

Вставьте пропущенные слова и допишите предложения. 1)При изготовлении фаянса сначала размеотчают и смешивают ____, ____ и ____. 2)Полученную смесь отправлют в____, где создаётся____ изделия 3)Для

Геометрия

2 года назад

ПОМОГИТЕ ПОЖАЛУЙСТА Вертикальными углами являются угол 3 и угол....

Русский язык

2 года назад

Помогите пожалуйста у меня тест 1.Определите на каком явлении лексики основывается данная пословица.Не учи безделью, а учи рукоделью использование синонимов использование антонимов использование

Математика

8 лет назад

вычислите значение выражения 3/8×7÷3; 5×1/5×100; 24/25÷6×25; 15/100÷3÷2

Алгебра

8 лет назад

Определить напровление ветвей параболы y=5x квадратной

География

9 лет назад

Для какой из перечисленных стран характерна аграрная структура хозяйства и почему? А) Украина Б) Турция В) Испания Г) Мьянма

Биология

9 лет назад

Отличие днк от гена??? ПЛИЗ!!!