постройте график функции y = 2 - (4x^ - 16x) / (x^3 - 4x^2)

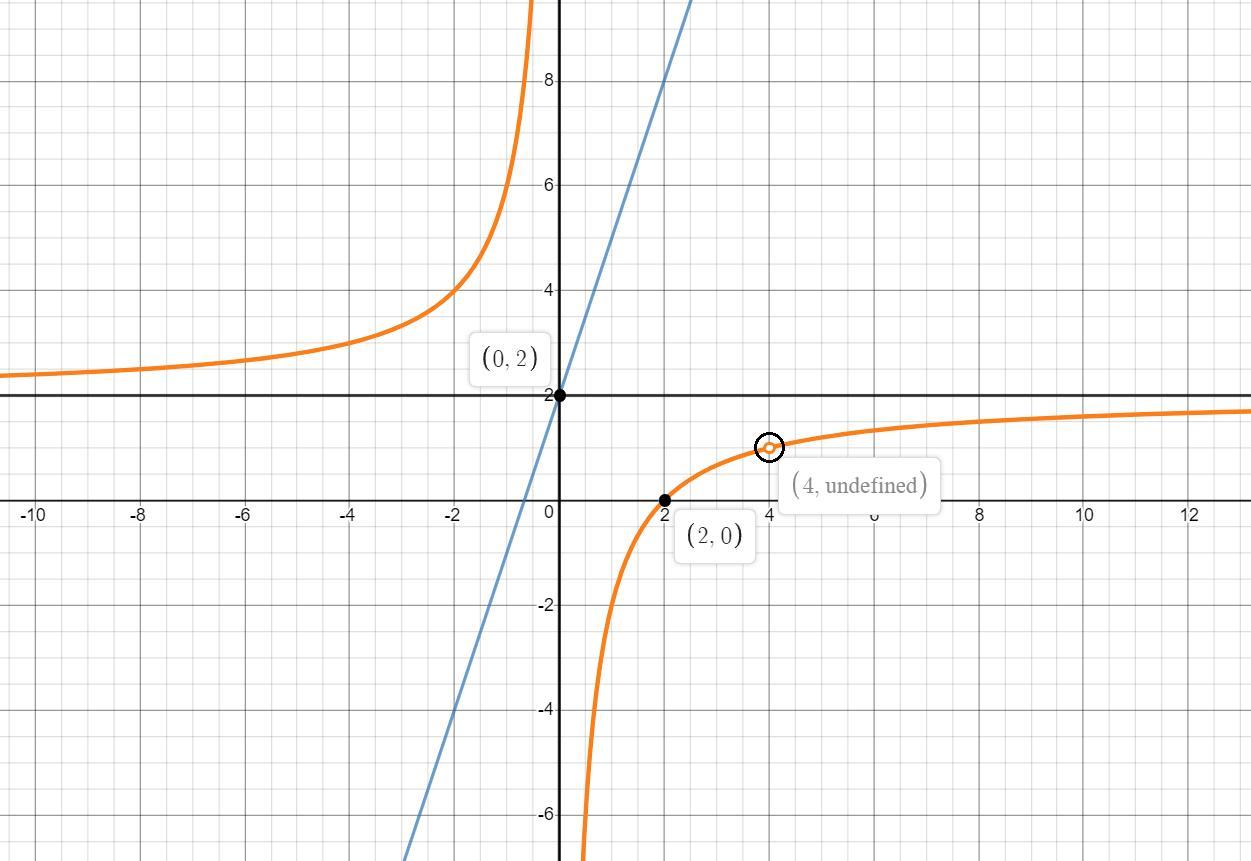
Это гипербола асимптоты которой: x=0 и y=2. Лежит во 2 и 4 четверти относительно асимптот. И так же в точке (4;1) функция не определена.

Точки пересечения:

Когда а=0, то получается у=2, если будет чуть меньше 2, то уже будет пересекать т.к. асимптота это у=2. Если а будет очень большим, то прямая будет стремиться к тому, чтобы слиться с x=0, но в любом случаи х=0 это асимптота, проще говоря прямая не будет пересекать гиперболу в тех четвертях где нету самой гиперболы, то есть в 1 и 3. Значит 0≤a<+∞. Так же функция не определена в точке (4;1), но в любом случаи будучи в 4 четверти, прямая будет и во 2, а значит пересечёт гиперболу.

Ответ: [0;+∞)