Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно, АВ=28, АС=24, MN=18. Найдите АМ.
Приложения:
Ответы
Ответ дал:
0
Если прямая MN параллельна стороне AC, то треугольники подобны.(так, как у них равные углы). Коэффициент подобия k равен: AC/MN = 24/18 = 1,3. Теперь находим сторону BM, она равна: AB/k = 28/1,3 = 21,5 см Значит АМ равно: AB - BM = 28 - 21,5 = 6,5 см
Ответ: АМ = 6,5 см
Стоит отметить, что значения k, BM, и AM я округлил до десятых, так, как получаются не целые результаты.
Ответ дал:
0
нельзя округлять. нужно решать дробями.
Ответ дал:
0
А как изменить ответ? Что-то я кнопки "изменить" найти не могу.
Ответ дал:
0
она активна только в течении одного часа с момента написания ответа.
Ответ дал:
0
Понял, спасибо.
Ответ дал:
0
помогите пожалуйста https://znanija.com/task/32029119
Ответ дал:
0
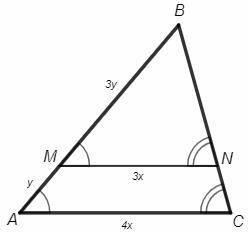
Соответственные углы при параллельных равны,
△MBN~△ABC (по двум углам)
MB/AB=MN/AC =18/24 =3/4
AM/AB =(AB-MB)/AB =1 -3/4 =1/4 => AM=AB/4 =28/4 =7
Приложения:
Ответ дал:
0
помогите пожалуйста https://znanija.com/task/32029119
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад