Помоги по братски
)))))))))))))))))))))))))))))))))))
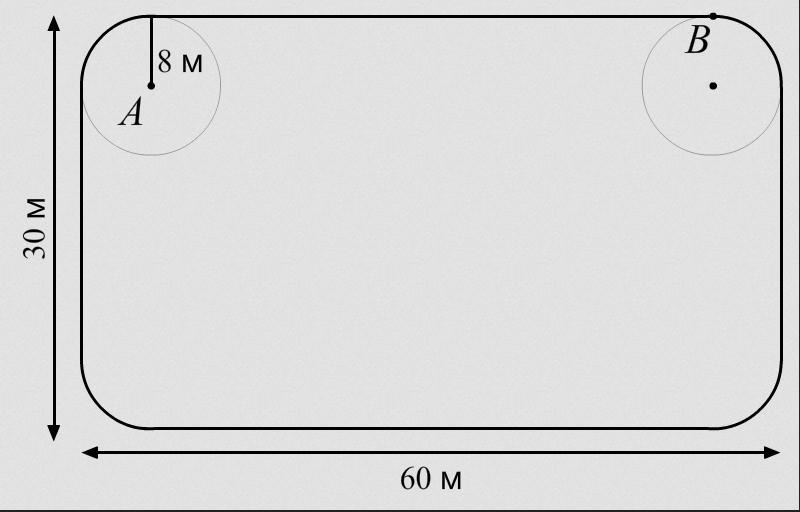
Хоккейная площадка имеет форму прямоугольника размером 60 м × 30 м с углами, закруглёнными по дугам окружностей радиуса 8 м. Вычислите скорость (м/с), с которой летит шайба от игрока, находящегося в точке A, до хоккеиста, который находится в точке B, если пас длится 1,8 с. Ответ округлите до целых.
https://edu.mob-edu.ru/ui/upload/courses/1944590/files/web_resources/13/images/8_13_2/Geom_8_13_2_7.png
Ответы
Ответ дал:
0
Расстояние между А и В является диагональю прямоугольного треугольника с катетами:
а = 60 - 2·8 = 44 (м) и b = 8 (м)
Тогда: S = √(a²+b²) = √(1936+64) = √2000 ≈ 44,72 (м)
Скорость шайбы:
v = S/t = 44,72 : 1,8 ≈ 24,85 (м/с) = 89,44 (км/ч)
Приложения:
Ответ дал:
0
Больший катет - расстояние между центрами окружностей.
Ответ дал:
0
Каждый центр отстоит от борта по длине на 8 м.
Ответ дал:
0
Значит, расстояние между центрами окружностей будет меньше длины на 2·8=16 метров.
Ответ дал:
0
спс
Ответ дал:
0
Да не за что...))
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад