Ответы
Ответ дал:
0
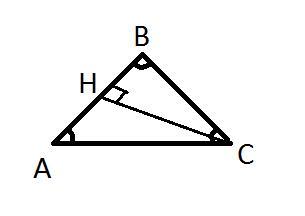
Так как у нас равносторонний треугольник - все углы по 60°, по-этому нет разницы с какой вершины проведена высота - она будет проведена на сторону между равными сторонами. Рассмотрим Δ ВСА, так как ВС=СА - он равнобедренный, а СН - высота на сторону между ними.
ВН = НА = 0.5* ВА (за способностью высоты в равнобедренном треугольнике)
Рассмотрим ΔВСН:
Пусть ВС - х, тогда ВН - 0.5 х , СН - 3см (по условию)
По теореме Пифагора:
х² = (3)² + (0.5х)²
х² = 9 + 0.25х²
Треугольник равносторонний, ВС = ВА = 2√3 см
Приложения:
Ответ дал:
0
Ты гений))
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад