• Предмет: Математика
  • Автор: frantsuziii
  • Вопрос задан 7 лет назад
< >

Решите неравенство 1/(2x+3)^2≥4

Ответы

Ответ дал: Dakota13
0

Ответ:

...........................

Пошаговое объяснение:

Приложения:
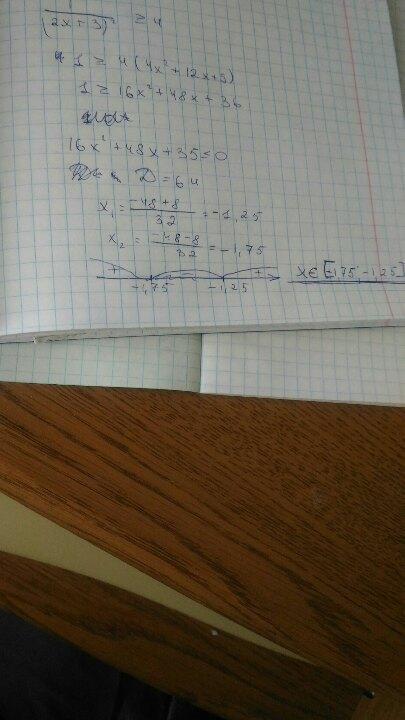
Ответ дал: ndehost
0

frac{1}{(2x+3)^2}geq4|*(2x+3)^2\ xneq -frac{3}{2}; xneq-1.5\1geq 4(2x+3)^2\4(2x+3)^2leq 1\4(4x^2+12x+9)leq 1\16x^2+48x+36leq 1\16x^2+48x+36-1leq 0\16x^2+48x+35leq 0\D^2=48^2-4*16*35=2304-2240=64; D=sqrt{64}=+-8\ x_1=frac{-48+8}{2*16}=frac{-40}{32}=frac{-10}{8}=-frac{5}{4}=-1.25\\x_2=frac{-48-8}{2*16}=frac{-56}{32}=-frac{7}{4}=-1.75\16(x+1.25)(x+1.75)leq 0\

 (+)                 (-)                (+)

____-1.75______-1.25___0

xє[ -1.75;-1.25]

Приложения:
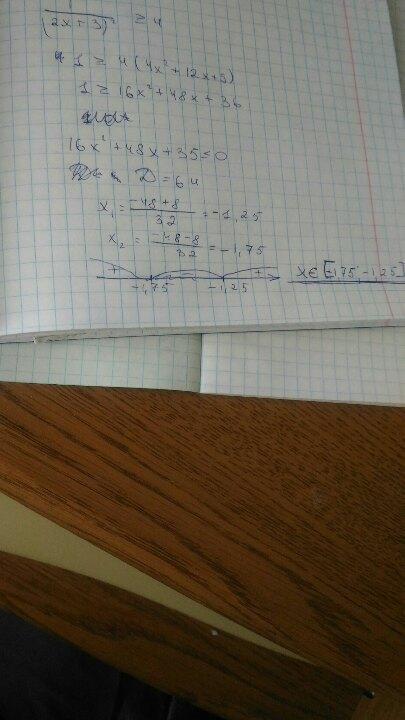
Похожие вопросы
Русский язык
1 год назад
Даль беспокойнуюю указать род и падеж
Русский язык
1 год назад
Помоги дождику составить обьявление
Математика
2 года назад
математика помогите пожалуйста ​
Математика
2 года назад
срочно!!!!!! соотношение сторон треугольника равно 3 : 6 : 7. определи длины сторон треугольника, если периметр треугольника равен 80дм!
Физика
8 лет назад
Вдавливая кнопку в доску,на неё по действовали силой 50Н.Площадь острия кнопки равна 0,1 мм^2.Найдите производимое ею давление.
Математика
8 лет назад
Высота треугольника АВС равна √6 см, угол А равен 45°, угол С равен 60°. Найдите площадь треугольника АВС.
Математика
9 лет назад
Длина прямоугольника в 3 раза больше его ширины а периметр равен 32 см Найди длину и ширину прямоугольника
Математика
9 лет назад
2/3x+5/9x-1/3=7/9 помогите решить уравнение