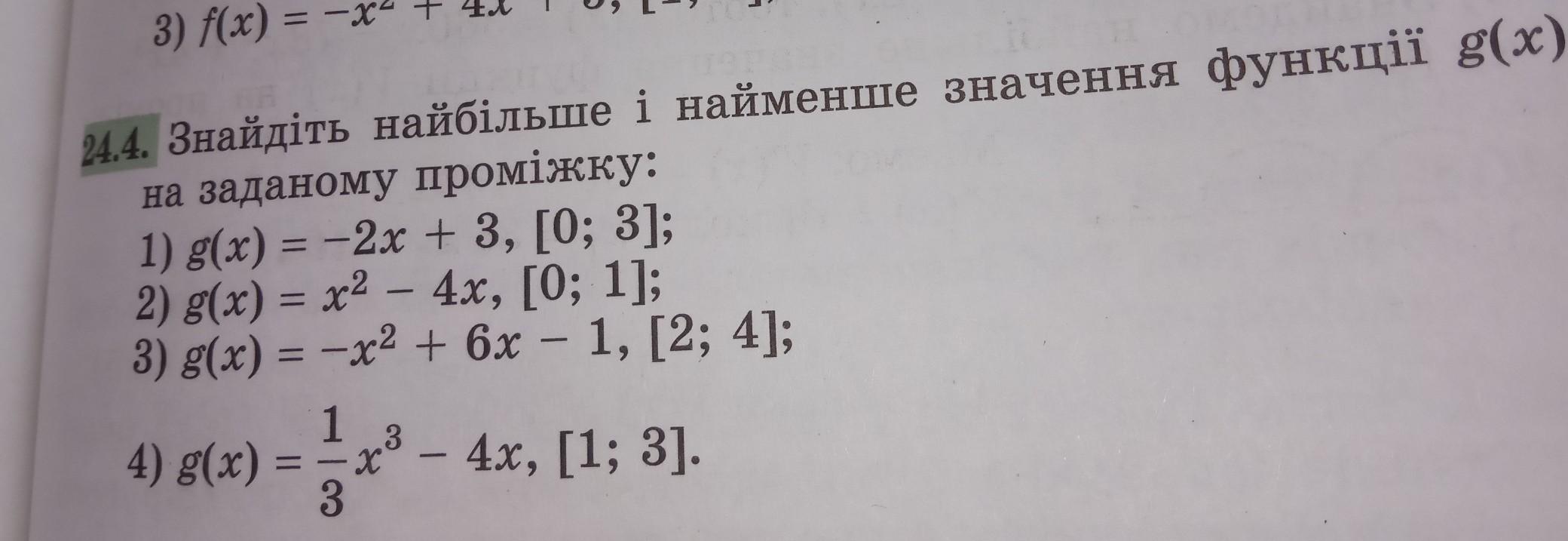Ответы
Ответ дал:
0
1)

g(x) = -2x+3
[0;3]
Находим первую производную функции:
g' (x)= -2
Приравниваем ее к нулю:
-2 ≠ 0
Глобальных экстремумов нет
Находим стационарные точки:
Вычисляем значения функции на концах отрезка
g(0) = 3
g(3) = -3
Ответ:
Имеются только локальные экстремумы (на заданном интервале)
g min = -3, g max = 3
2)

Экстремумы функции
g(x) = x^2-4x
[0;1]
Находим первую производную функции:
g' (x)= 2x-4
Приравниваем ее к нулю:
2x-4 = 0
x1 = 2
Вычисляем значения функции на концах отрезка
g(2) = -4
g(0) = 0
g(1) = -3
Ответ:
g min = -3, g max = 0
3)

Экстремумы функции
g(x) = -x^2+6x-1
[2;4]
Находим первую производную функции:
g' (x)= -2x+6
Приравниваем ее к нулю:
-2x+6 = 0
x1 = 3
Вычисляем значения функции на концах отрезка
g(3) = 8
g(2) = 7
g(4) = 7
Ответ:
g min = 7, g max = 8
4)

g(x) = (1/3)*x^3-4*x
[1;3]
Находим первую производную функции:
g' (x)= x^2-4
Приравниваем ее к нулю:
x^2-4 = 0
x1 = -2
x2 = 2
Вычисляем значения функции на концах отрезка


Ответ:

g(x) = -2x+3
[0;3]
Находим первую производную функции:
g' (x)= -2
Приравниваем ее к нулю:
-2 ≠ 0
Глобальных экстремумов нет
Находим стационарные точки:
Вычисляем значения функции на концах отрезка
g(0) = 3
g(3) = -3
Ответ:
Имеются только локальные экстремумы (на заданном интервале)
g min = -3, g max = 3
2)
Экстремумы функции
g(x) = x^2-4x
[0;1]
Находим первую производную функции:
g' (x)= 2x-4
Приравниваем ее к нулю:
2x-4 = 0
x1 = 2
Вычисляем значения функции на концах отрезка
g(2) = -4
g(0) = 0
g(1) = -3
Ответ:
g min = -3, g max = 0
3)
Экстремумы функции
g(x) = -x^2+6x-1
[2;4]
Находим первую производную функции:
g' (x)= -2x+6
Приравниваем ее к нулю:
-2x+6 = 0
x1 = 3
Вычисляем значения функции на концах отрезка
g(3) = 8
g(2) = 7
g(4) = 7
Ответ:
g min = 7, g max = 8
4)
g(x) = (1/3)*x^3-4*x
[1;3]
Находим первую производную функции:
g' (x)= x^2-4
Приравниваем ее к нулю:
x^2-4 = 0
x1 = -2
x2 = 2
Вычисляем значения функции на концах отрезка
Ответ:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад