определите вид треугольника ABC если его вершины имеют координаты: (координаты на фотографии) пошаговое решение пожалуйста
Приложения:
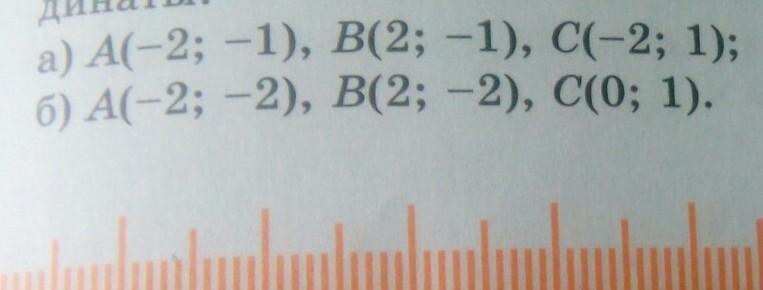
Ответы
Ответ дал:
0
Нужно сравнить длины сторон треугольников
Для этого находим их по формуле расстояния между двумя точками
d=√((x2-x1)^2+(y2-y1)^2)
a)
AB=√((2+2)^2+(-1+1)^2)=√(16)=4
BC=√((-2-2)^2+(1+1)^2)=√(16+4)=√20
CA=√((-2+2)^2+(-1-1)^2)=√(4)=2
Стороны не равны, но сторона BC больше остальных, поэтому проверим выполняется ли на них теорема пифагора
(√20)^2=2^2+4^2
20=4+16
20=20
Теорема Пифагора выполняется, значит треугольник прямоугольный.
б)
AB=√((2+2)^2+(-2+2)^2)=√(16)=4
BC=√((0-2)^2+(1+2)^2)=√(4+9)=√13
CA=√((-2-0)^2+(-2-1)^2)=√(4+9)=√13
т.к. равны 2 стороны, то треугольник равнобедренный.
Ответ дал:
0
по формуле АВ=√(х2 - х1)² + (у2 - у1)²
мы решаем и в а) у нас получается прямоугольный треугольник, а в б) равнобедренный
Похожие вопросы
2 года назад
8 лет назад