Ответы
Ответ:
18 см^2
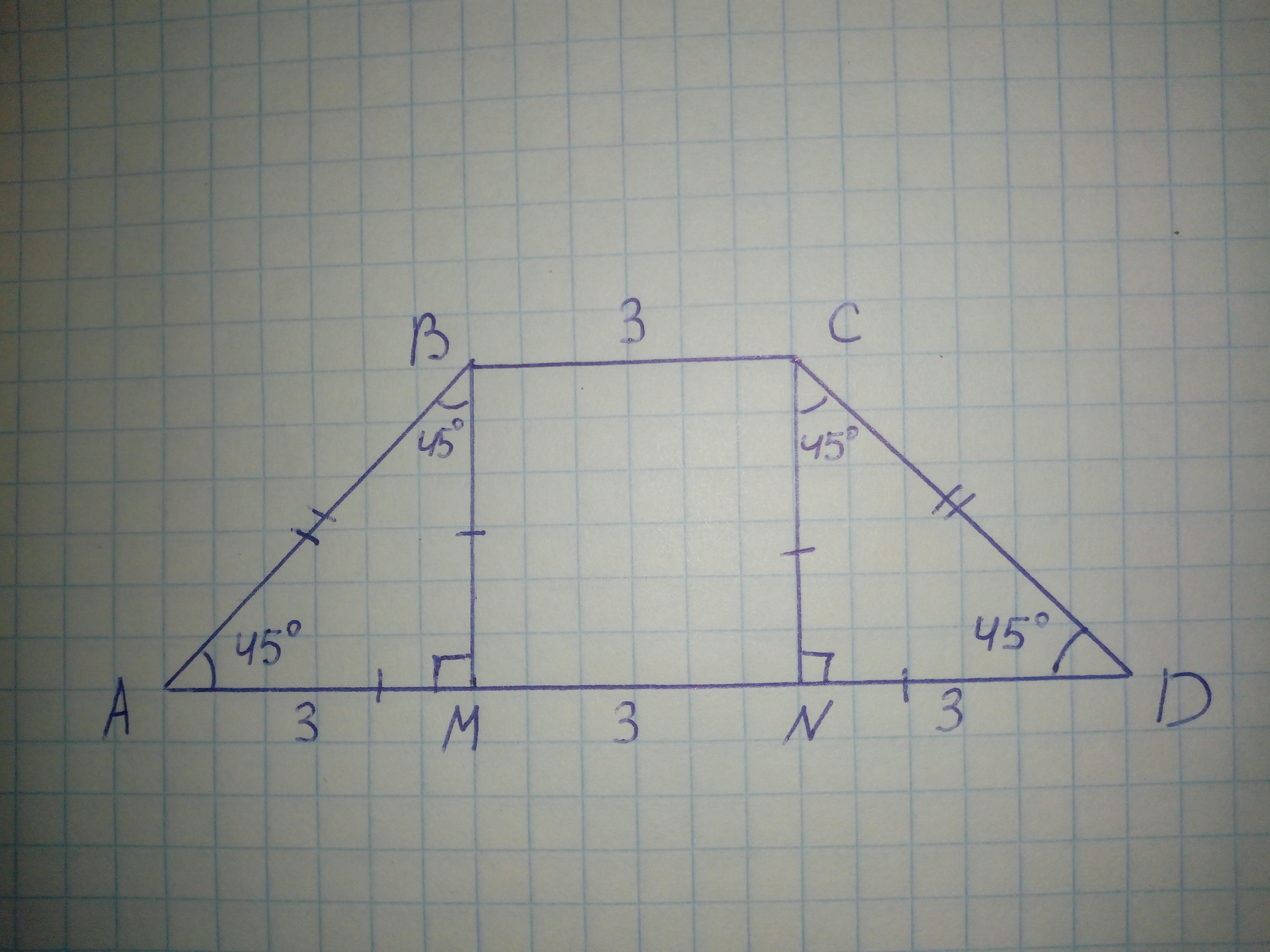
1. Докажем что трапеция равнобедренная, опустим высоты из вершин верхнего основания
2. найдем разницу между основаниями и раздели ее на 2.
3. Рассмотрим треугольник треугольник сформированный из высоты, одной боковой стороной и "катет - разнице между основаниями деленной на 2". этот треугольник равнобедренный, прямоугольный в котором катет равен высоте = (9-3):2=3 см
4. S=(9+3):2*3=18 cм^2
Ответ:
18 см2.
Объяснение:
Проведём высоты BM и CN. Трапеция равнобедренная, следовательно углы A и D равны
(по 45°).
Рассмотрим треугольники ABM и NCD. Углы ABM и NCD тоже равны (90° - 45° = 45°); треугольники равнобедренные. Поскольку они равнобедренные, высоты BM и CN равны AM и ND (AM = ND).
MN = BC = 3. Пускай AM и ND = x. Тогда:
2x = 9 - 3 =6
x = 3
Значит высота тоже равна 3.
S трапеции = 0.5*(a+b)*h
S трапеции (ABCD) =0.5*(3+9)*3 = 6*3 = 18 см2