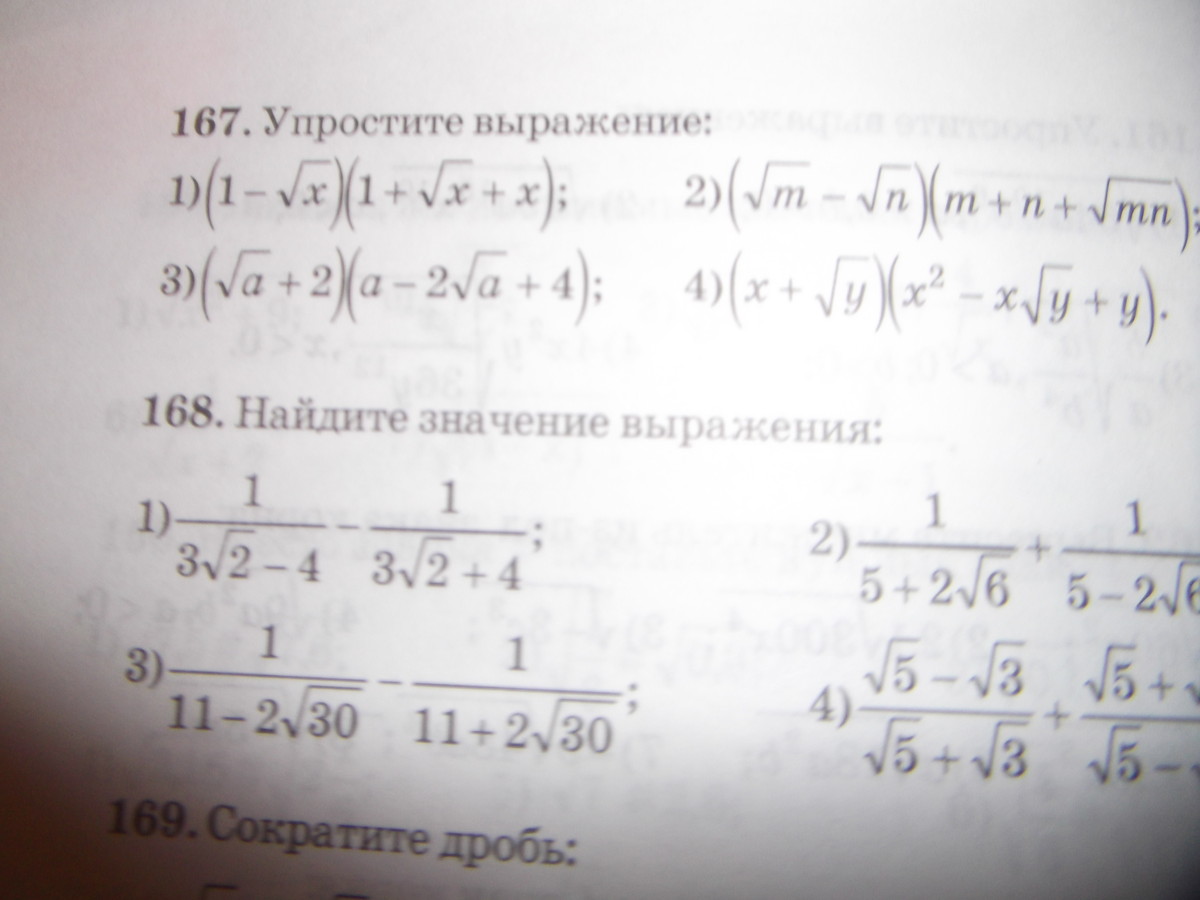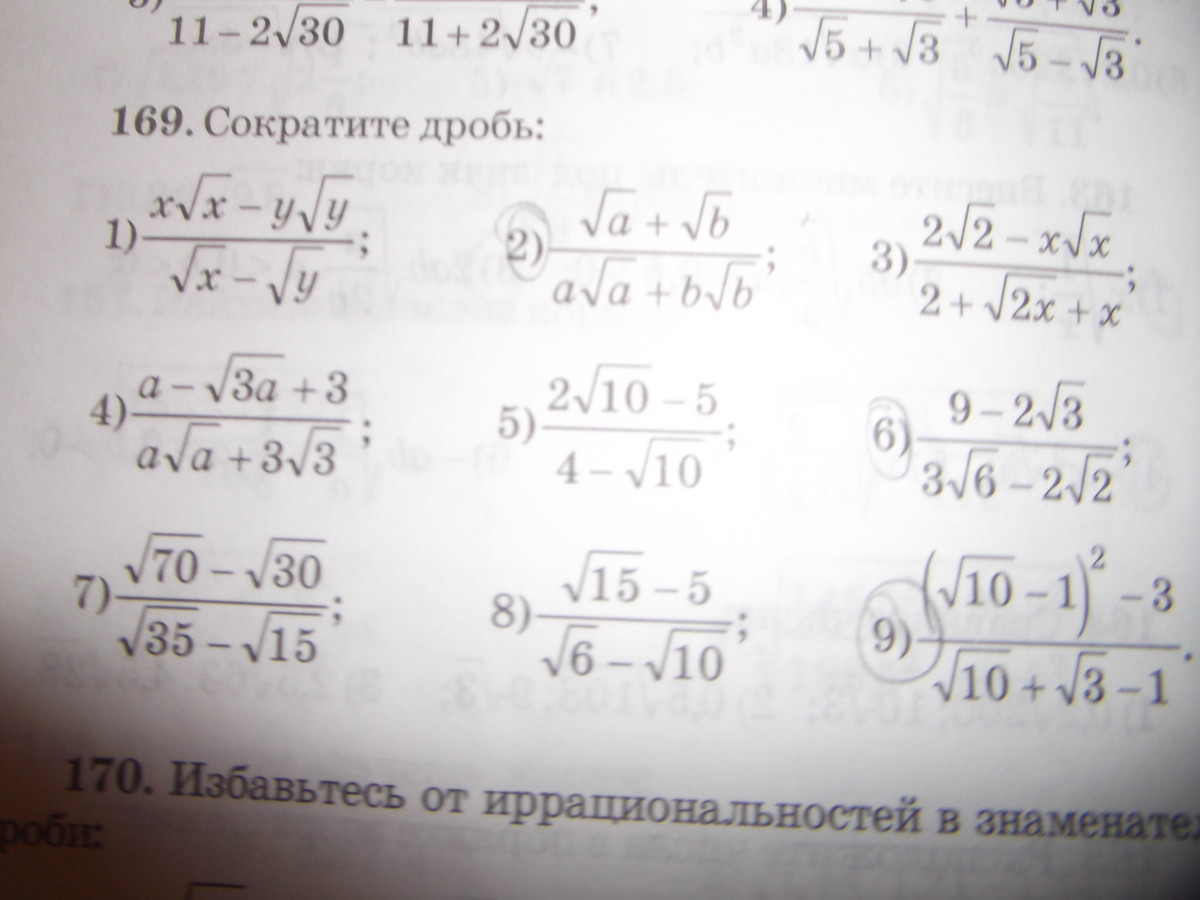Предмет: Алгебра
Автор: Аноним
Вопрос задан 10 лет назад

Решите №169(2,6,9).№167(1,2).

Приложения:

Ответы

Ответ дал: Света19999

167.
1) 1 - (√x)^3
2) (√a)^3 + 8

169.
2)(√a+√b)/(a√a + b√b) =(√a+√b)/((√a)^3 + (√b)^3) = (√a+√b)/(√a+√b)(a - √ab + b) = = 1/(a - √ab + b) = (a - √ab + b)^ -1

Ответ дал: Аноним

можно картинкой и подробнее

Ответ дал: Artem112

$(1- sqrt{x} )(1+ sqrt{x} +x)=1-x sqrt{x} \ ( sqrt{m} - sqrt{n} )(m+n+ sqrt{mn} )=msqrt{m} -n sqrt{n}$

$frac{ sqrt{a}+ sqrt{b} }{a sqrt{a}+b sqrt{b} } = frac{ sqrt{a}+ sqrt{b} }{(sqrt{a}+ sqrt{b} )(a+b- sqrt{ab}) } =frac{ 1 }{a+b- sqrt{ab} }$

$frac{9-2 sqrt{3} }{3 sqrt{6}-2 sqrt{2} } = frac{ sqrt{3}(3 sqrt{3}-2) }{sqrt{2} (3 sqrt{3}-2 ) } = frac{ sqrt{3} }{sqrt{2} } = sqrt{1.5}$

$frac{( { sqrt{10}-1)^2-3} }{ sqrt{10}+ sqrt{3}-1 } = frac{ { (sqrt{10}-1- sqrt{3})(sqrt{10}-1+ sqrt{3}) } }{ sqrt{10}+ sqrt{3}-1 } =sqrt{10}-1- sqrt{3}$

Похожие вопросы

Русский язык

2 года назад

напишите пожалуйста сочнение !!!! (1)Любите ли вы литературу так, как люблю её я? (2)То есть любите ли вы читать книги? (3)Затратное занятие. (4)Но это как посмотреть. (5)Есть книги, не сокращающие

Русский язык

2 года назад

А1. В каком ряду все слова являются причастиями? 1) перевернув, посидев, невпопад, раскидистый 2) перепрыгнувший, решаемый, вынув, несчастный 3) гонимый, затемнена, нагретая, назначено

Алгебра

7 лет назад

помогите пожалуйста, нужна помощь

Алгебра

7 лет назад