Решите неравенство
(x+5)(2x-1)(x-3)<0

Ответ:

Пошаговое объяснение:

(x+5)(2x-1)(x-3) < 0

По методу интервалов решается мгновенно.

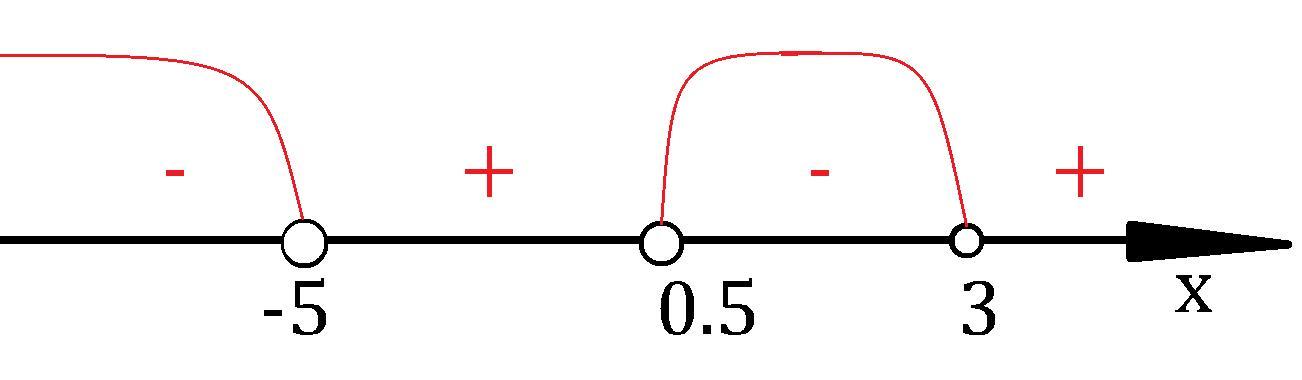
У нас есть особые точки (-5), 1/2 и 3.

Они делят числовую прямую на интервалы: (-oo; - 5); (-5; 1/2); (1/2; 3); (3; +oo).

Берем любое значение, например, 0, и подставляем.

(0+5)(2*0-1)(0-3) = 5(-1)(-3) = 15 > 0

Не подходит. Значит, отрезок, содержащий 0, (-5; 1/2) в решение не входит.

Зато входят два соседних интервала:

x € (-oo; - 5) U (1/2; 3)

не понятно конечно почему входят два соседних (из вашего объяснения) в случаи если бы знак в "особой точке" не менялся так бы не работало кто-то может подумать, что соседние и допускать ошибки в других заданиях из-за вашего объяснения

Разложили на множители, подготовив к методу интервалов.

Отмечаем на координатной прямой отмечаем точки в которых выражение равно нулю, но у нас строго меньше 0, поэтому эти точки мы выкалываем. Степени у корней все нечётные, а коэффициент при выражении положительный, поэтому чередуем + и - справа на лево, начиная с + и меняя знак при переходе через корень. ± говорит о знаке выражения (положительное/отрицательно), нас интересует когда меньше.

Смотри вниз.