в треугольнике авс вписана окружность с центром о. известно, что угол вас=40 градусов, угол авс=98 градусов. найдите угол всо. ответ дайте в градусах задача 8

В ΔABC найдем угол C:

∠C = 180° - 98° - 40° = 42°.

ΔMOC = ΔNOC по третьему признаку - по трем сторонам:

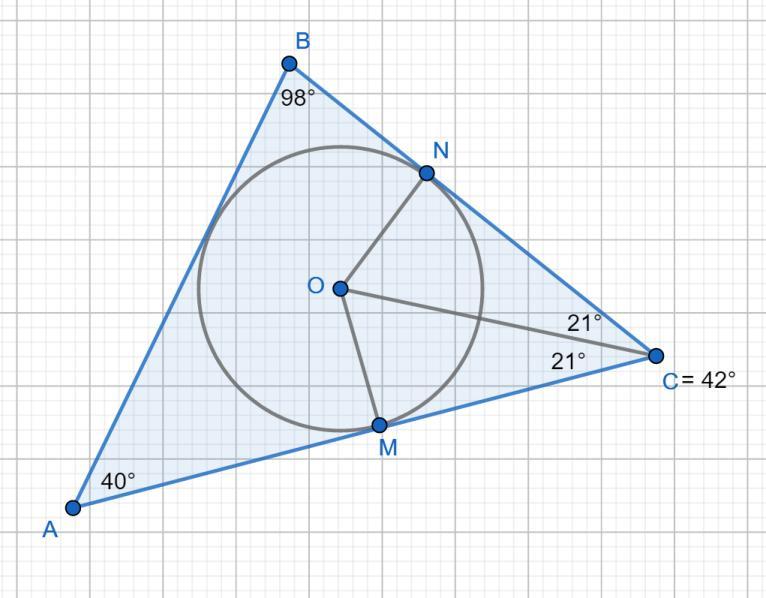
ON = OM радиусы вписанной окружности, NC = MC отрезки касательных, проведенных из одной точки до точек касания равны, OC общая сторона. ⇒∠NCO = ∠NCO

⇒ OC биссектриса. ∠BCO = 42°/2 = 21°

∠BCO = 21°