Помогите плз!!!!!!!!!
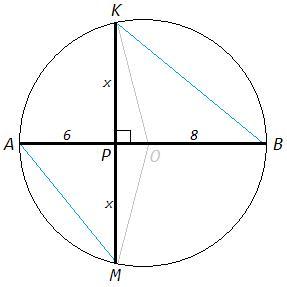
Диаметр AB окружности перпендикулярен хорде KM и пересекает её в точке P. Найдите длину хорды KM, если точка P делит диаметр на отрезки AP=6 см, PB=8 см.
ЕСЛИ НУЖЕН РИСУНОК ТО ЕГО НЕТУ
Ответы
Ответ дал:
0
Докажем свойство пропорциональности хорд.
A=K (вписанные углы, опирающиеся на дугу MB)
△APM~△KPB (по двум углам)
AP/KP=PM/PB <=> AP*PB=KP*PM
Диаметр, перпендикулярный хорде, делит ее пополам (△KOM - равнобедренный, OP - высота и медиана).
KP=PM =x
x^2 =6*8 <=> x=4√3
KM=2x =8√3
Приложения:
Ответ дал:
0
Другой способ. AKB - прямой (опирается на диаметр). Высота из прямого угла равна среднему пропорциональному проекций катетов, KP=V(AP*PB).
Ответ дал:
0
благодарю за решение
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад