Высота ромба, проведенная из вершины тупого угла, делит сторону пополам. Найдите меньшую диагональ, если периметр ромба равен 48 см.
Пожалуйста помогите :3

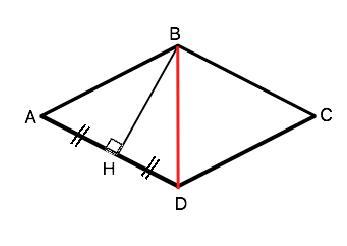
  Обозначим  ромб АВСD. Пусть угол АВС - тупой.

ВН- высота к стороне AD и   делит её пополам. Поскольку ВН не только высота. но и медиана, треугольник АВD- равнобедренный (свойство). ⇒ ВD=AB, а ∆ АВD - равносторонний, т.к. все стороны ромба равны.  

  АВ=48:4=12 см. Из доказанного выше  диагональ ВD=AB=12 см