Пожалуйста помогите ответить на это... Очень хочется разобраться что к чему)
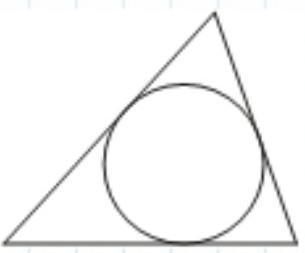
Периметр треугольника равен 50, одна из
сторон равна 20, а радиус вписанной в него
окружности равен 4. Найдите площадь этого
треугольника.
Простите рисунок не загружается(
Ответы
Ответ дал:
0
По третьему свойству вписанной окружности, радиус вписанной окружности равен: r=S/p, где S - площадь треугольника, а p - полупериметр. p=50/2=25 S=r*p=4*25=100
Ответ: 100
Приложения:
Ответ дал:
0
Спасибо за помощь))
Ответ дал:
0
;-)
Ответ дал:
0
Ответ:
100
Объяснение:
По третьему свойству вписанной окружности, радиус вписанной окружности равен: r=S/p,
где S - площадь треугольника,
p ( маленькая) - полупериметр.
p=50/2=25
S=r*p=4*25=100
Ответ: 100
Приложения:

Ответ дал:
0
Большое спасибо))
Ответ дал:
0
;-)
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад