Найти площадь фигуры ограниченной отрезками.


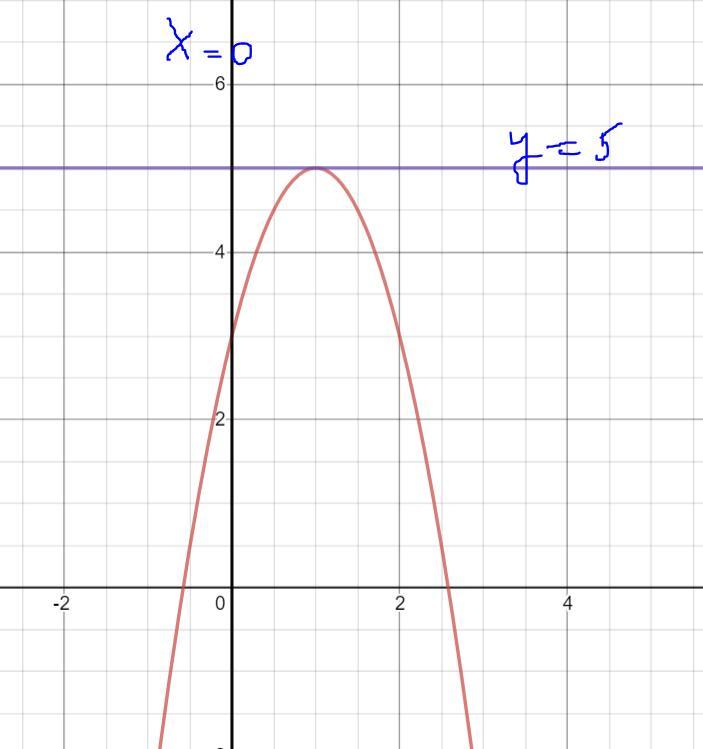
Функция: y = -2x^2 + 4x + 3

ограниченная прямыми:

y = 5

x = 0

Будем считать, что ограничением есть только х = 0, так как прямая у = 5 находится за пределами площади, ограниченной параболой  

y = -2x^2 + 4x + 3.

Для ограничения площади при пересечении параболой с осью Ох надо найти координаты точки пересечения параболы с осью Ох, при этом у = 0. Приравняем  -2x^2 + 4x + 3 = 0.   Д - 16 - 4*(-2)*3 = 40.

х = (-4 + √40)/(2*(-2)) = 1 +√(40/16) = 1 + √2,5 (правая точка).

Левую точку не определяем, так как задано х = 0.

Площадь определяем по интегралу: