Ответы
Ответ дал:
0
Ответ:
всё во вложении
Если что объясню точка макс. -9 т.к. условие для этой точки должно быть такое:
f(x)<f(x0)
А по определению x0=0 или не существует
Приложения:
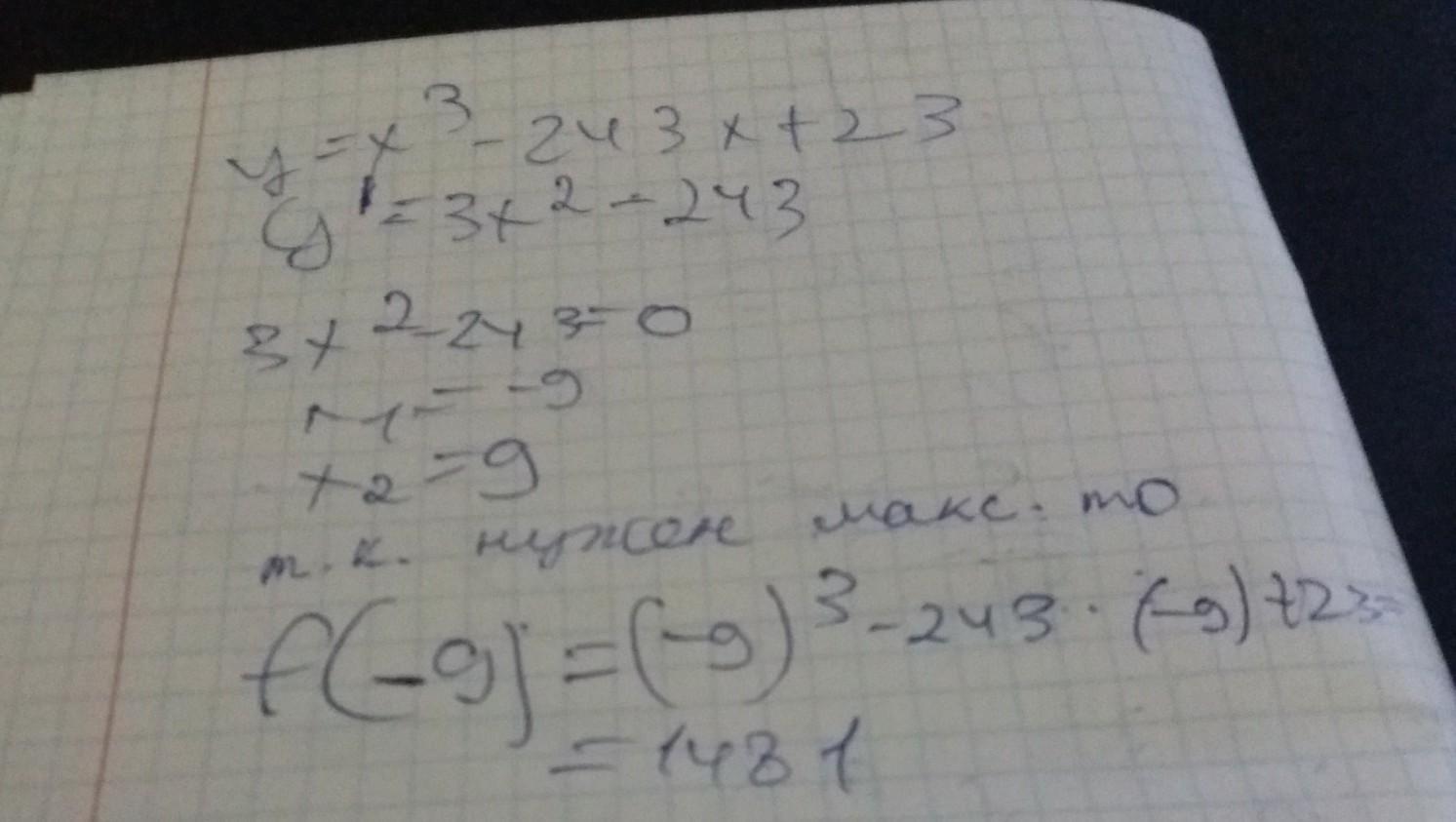
Ответ дал:
0
Что зря?
Ответ дал:
0
зря просите лучший ответ. Вы же даже не делаете пояснений в задачах. Понимает ли тот, кому вы пишете, почему не берется 9? Откуда он это может знать, если вы ему не объясните, но в своих решениях вы даже не делаете таких попыток. Поэтому зря..
Ответ дал:
0
с вашей точки так
Ответ дал:
0
точки зрения
Ответ дал:
0
а с Вашей? КАК человек может догадаться, дойти до Вашего решения? Или ему не важно, как решалось, главное верный ответ?
Ответ дал:
0
1. Находим производную функции. 3х²-243
2. Определяем критические точки функции. 3х²-243=0, х=±√81=±9
3. На интервалы критические точки разбивают область определения;
4. Устанавливаем знаки производной на каждом интервале с помощью метода интервалов.
___-9______9________
+ - +
Максимума функция достигает в точке х=-9 и равен он
(-9)³-243*(-9)+23=-729+2187+23=1481
Приложения:
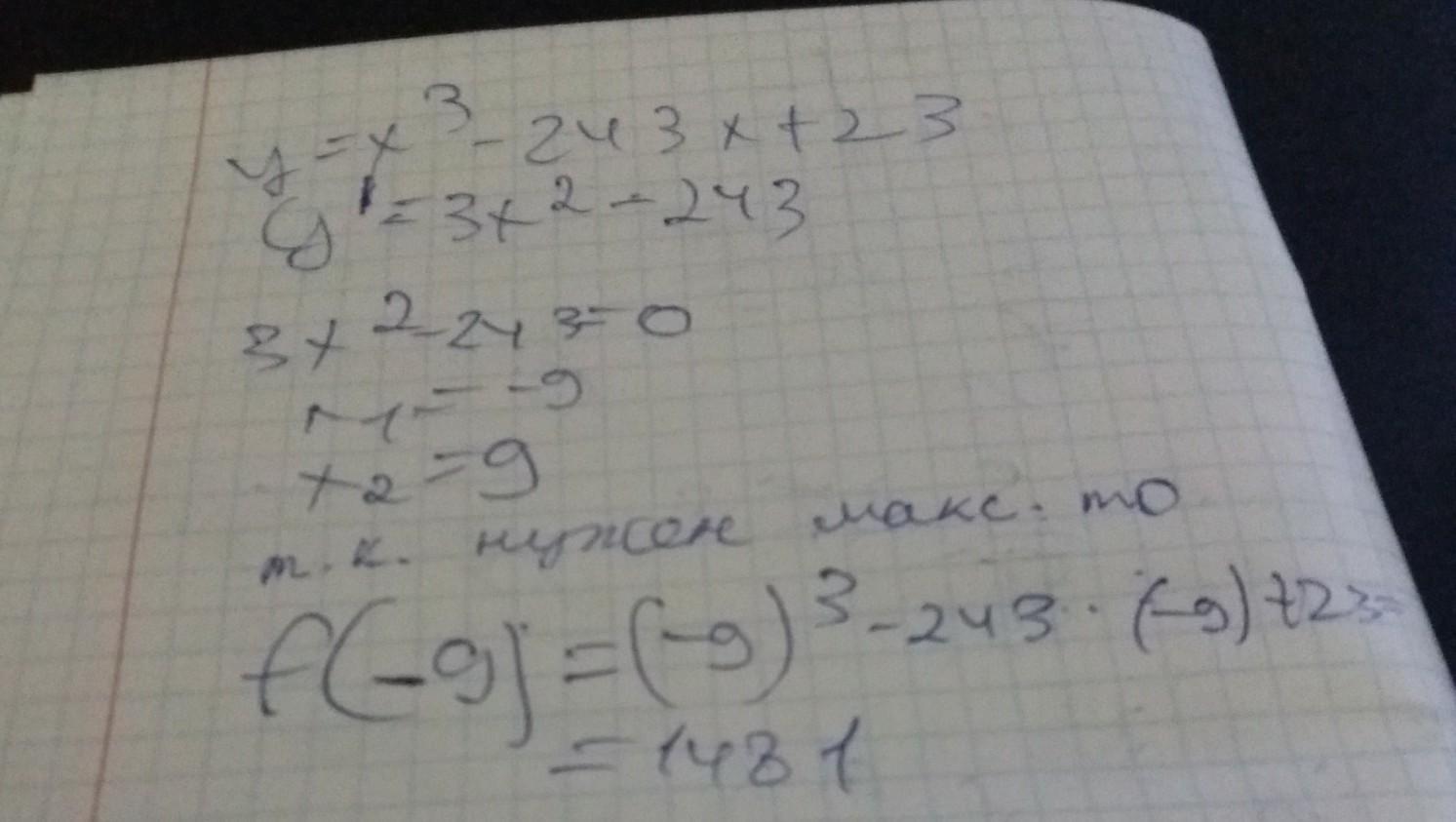
Похожие вопросы
1 год назад
1 год назад
2 года назад
8 лет назад
9 лет назад