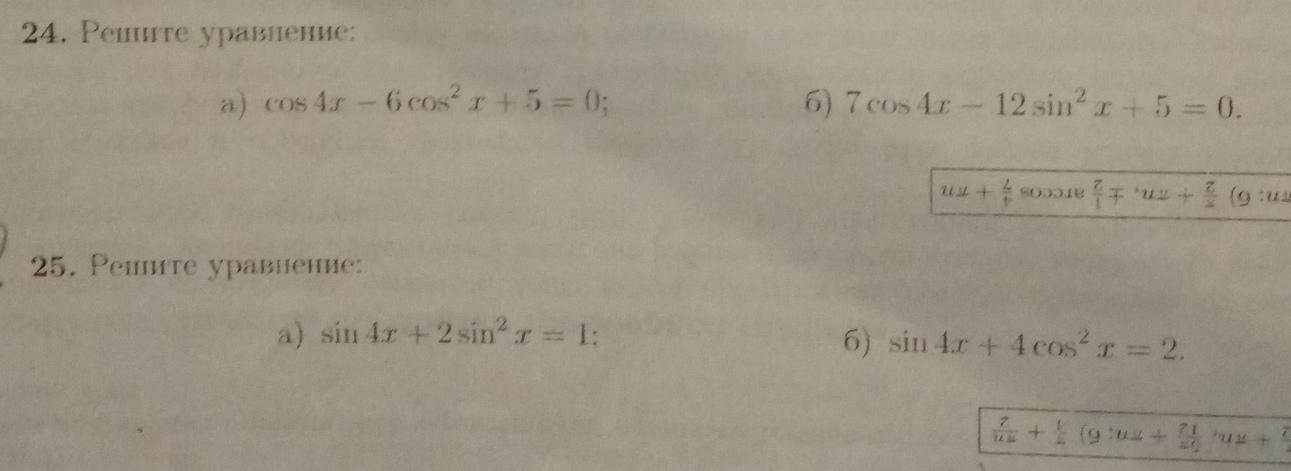Предмет: Математика
Автор: senyatrusov
Вопрос задан 7 лет назад

< >

Помогите решить пожалуйста)))

Приложения:

Ответы

Ответ дал: Guerrino

0

24)

а) Сделаем несколько равносильных преобразований: $cos4x-6cos^{2}x+5=0 Leftrightarrow cos4x+6(1-cos^{2}x)=1 Leftrightarrow cos4x+6sin^{2}x=1$ ; Теперь поделим обе части уравнения на 3:

$frac{cos4x}{3}+2sin^{2}x=1-frac{2}{3}Leftrightarrow frac{cos4x}{3}-cos2x+frac{2}{3}=0 Leftrightarrow cos4x-3cos2x+2=0$ ; Сделаем замену: t=2x; $cos2t-3cos t+2=0 Leftrightarrow 2cos^{2}t-3cos t+1=0$ ; Делаем замену: m=cos(t); $2m^{2}-3m+1=0 Leftrightarrow m=1,; m=0.5$ ; Возвращаясь к замене и решая простейшее триг. уравнение, получаем: $t=2pi k,; t=frac{pi}{3}+2pi l,; t=frac{5pi}{3}+2pi l,; k,l in mathbb{Z}$ ; Отсюда $x=pi k,; x=frac{pi}{6}+pi l,; x=frac{5pi}{6}+pi l,; k,l in mathbb{Z}$

б) здесь все то же: $7cos4x-12sin^{2}x+6=1 Leftrightarrow 7cos4x+6cos2x-1=0$ ; После тех же самых бесчисленных замен приходим к ответу: $x=frac{pi}{2}+kpi,; x=pmfrac{1}{2}arccos(frac{4}{7})+pi n,; k,nin mathbb{Z}$

25)

а) $sin4x=1-2sin^{2}xLeftrightarrow sin4x=cos2x$

Возможно лишь два случая: $frac{pi}{2}+2pi k-4x=2x ;; textbf{or};; 4x=frac{pi}{2}+2pi k+2x Rightarrow x=frac{pi}{12}+frac{pi k}{3},; x=frac{pi}{4}+frac{pi k}{2},; kinmathbb{Z}$

б)

$sin4x=2(1-2cos^{2}x) Leftrightarrow sin4x = -2cos2x Leftrightarrow sin2xcos2x=-cos2x$ ; Вынесем за скобку:

$cos2x(sin2x+1)=0$ ; Простейшие триг. уравнения:

$cos2x=0,; sin2x=-1$

Ответ: $x=frac{pi}{4}+frac{pi k}{2},; x=frac{3pi}{4}+pi k,; kinmathbb{Z}$

Похожие вопросы

Русский язык

2 года назад

Помогите составить 5 нечленимых словосочетаний

Русский язык

2 года назад

реСкачавшиеся почему с тросТников почему пишем букву т

Литература

2 года назад

Какое произведение принесло известность фету

Другие предметы

2 года назад

підпишіть порції раціонального харчування на основі піраміди здоров'я

Химия

8 лет назад

Металлы взаимодействуют с солями,Если они обладают...химической активностью и расположены в ряду активности металлов...металла,ионы которого входят в состав соли

Математика

8 лет назад

Определите масштаб карты, если расстояние между двумя пунктами на местности 750м а на карте 25мм

Математика

9 лет назад

сколько будет x в квадрате плюс игрек равно единице сколько будет икс в квадрате плюс игрек в квадрате равно единице

Обществознание

9 лет назад

"Настоящий друг с тобой, когда ты не прав. Когда ты прав,всякий будет с тобой" Приведите 2 случая из жизни.